| ... """Sum of two dependent variables."""
from pylab import legend, figure, title
from pacal import *
|
||
|
.
|
||
Using compiled interpolation routine Compiled sparse grid routine not available
| ... X = UniformDistr(1, 2, sym="X")
Y = BetaDistr(2, 2, sym="Y")
U = X + Y
U.setSym("U")
colors = "kbgrcmy"
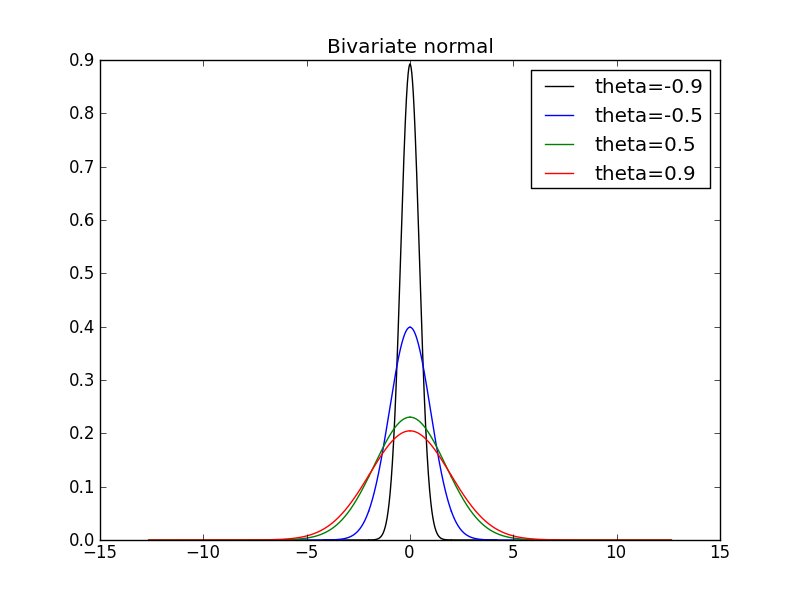
title("Bivariate normal")
for i, theta in enumerate([-0.9, -0.5, 0.5, 0.9]):
print "theta=", theta
ci = NDNormalDistr([0, 0], [[1, theta],[theta, 1]])
Mi = TwoVarsModel(ci, ci.Vars[0] + ci.Vars[1])
funi = Mi.eval()
funi.plot(label = "theta={0}".format(theta), color = colors[i])
funi.summary()
|
||
|
.
|
||
theta= -0.9
============= summary =============
PDISTR(-inf,inf)
mean = -8.4076490344461852e-17
var = 0.19999999999999996
skewness = 1.5470381899813639e-15
kurtosis = 2.9999999999999947
entropy = 0.61421957698762208
median = 0.0
mode = 7.44960108190967e-09
medianad = 0.3016409863130577
iqrange(0.025) = 1.7530450811531637
ci(0.05) = (-0.8765225405765831, 0.8765225405765806)
range = (-inf, inf)
tailexp = (0, 0)
int_err = -6.6613381477509392e-16
theta= -0.5
============= summary =============
PDISTR(-inf,inf)
mean = 0.0
var = 1.0000000000000002
skewness = 3.8857805861880464e-16
kurtosis = 3.0000000000000013
entropy = 1.4189385332046736
median = 0.0
mode = 2.273415680150447e-08
medianad = 0.6744897501960816
iqrange(0.025) = 3.9199279690800957
ci(0.05) = (-1.959963984540053, 1.9599639845400427)
range = (-inf, inf)
tailexp = (-235.71613043125419, -235.71613043125419)
int_err = -6.6613381477509392e-16
theta= 0.5
============= summary =============
PDISTR(-inf,inf)
mean = 2.2204460492503131e-16
var = 3.0000000000000027
skewness = 0.0
kurtosis = 2.9999999999999987
entropy = 1.9682446775387281
median = 0.0
mode = 3.2760631161472527e-08
medianad = 1.1682505165240524
iqrange(0.025) = 6.789514404457014
ci(0.05) = (-3.394757202228517, 3.3947572022284973)
range = (-inf, inf)
tailexp = (-78.572043477084733, -78.572043477084748)
int_err = -6.6613381477509392e-16
theta= 0.9
============= summary =============
PDISTR(-inf,inf)
mean = 5.5511151231257827e-17
var = 3.8000000000000034
skewness = 1.1990155676335915e-16
kurtosis = 2.9999999999999996
entropy = 2.0864390665708443
median = 0.0
mode = 2.6029869451932192e-08
medianad = 1.3148225765685222
iqrange(0.025) = 7.641346352217874
ci(0.05) = (-3.8206731761088686, 3.8206731761090054)
range = (-inf, inf)
tailexp = (-284.96125040713093, -284.96125040713105)
int_err = -6.6613381477509392e-16
| ... legend()
show()
|
||
|
.
|
||
| ... figure()
title("GumbelCopula")
for i, theta in enumerate([1, 5, 10, 15]):
print "theta=", theta
ci = GumbelCopula(marginals=[X, Y], theta=theta)
Mi = TwoVarsModel(ci, U)
funi = Mi.eval()
funi.plot(label = "theta={0}".format(theta), color = colors[i])
funi.summary()
|
||
|
.
|
||
theta= 1
============= summary =============
PDISTR(1.0,3.0)
mean = 1.9999999999999998
var = 0.13333333333333333
skewness = 1.9953090755351639e-15
kurtosis = 2.410714285714286
entropy = 0.39609176287256442
median = 2.0
mode = 1.9999999662226453
medianad = 0.2663852521625171
iqrange(0.025) = 1.38151947132566
ci(0.05) = (1.3092402643371701, 2.69075973566283)
range = (1.0, 3.0)
tailexp = (None, None)
int_err = 1.1102230246251565e-16
theta= 5
============= summary =============
PDISTR(1.0,3.0)
mean = 1.9999999951707179
var = 0.25482305407741646
skewness = 0.020576292821770339
kurtosis = 1.9455234190728341
entropy = 0.64307641687453254
median = 1.9953587437002176
mode = 1.9130523565037458
medianad = 0.416055594134902
iqrange(0.025) = 1.7448638985136915
ci(0.05) = (1.1335946904966798, 2.8784585890103713)
range = (1.0, 3.0)
tailexp = (None, None)
int_err = -7.9211193160233506e-10
theta= 10
============= summary =============
PDISTR(1.0,3.0)
mean = 1.9999997112993448
var = 0.26009603510786028
skewness = 0.0058464049709241548
kurtosis = 1.9335745577335595
entropy = 0.64882780413091501
median = 1.9987028905108615
mode = 1.9754600343288466
medianad = 0.42187205230061176
iqrange(0.025) = 1.7567466849594569
ci(0.05) = (1.1234359061296857, 2.8801825910891425)
range = (1.0, 3.0)
tailexp = (None, None)
int_err = 9.6046346875766631e-08
theta= 15
============= summary =============
PDISTR(1.0,3.0)
mean = 1.9999996736712253
var = 0.26109680319935952
skewness = 0.0027051874111487292
kurtosis = 1.9318390833294485
entropy = 0.6499245096916122
median = 1.9994065499403808
mode = 1.9889611374005454
medianad = 0.42287900167849546
iqrange(0.025) = 1.7592406838435208
ci(0.05) = (1.1212353827462243, 2.880476066589745)
range = (1.0, 3.0)
tailexp = (None, None)
int_err = 1.0873587541482266e-07
| ... legend()
show()
|
||
|
.
|
||

| ... figure()
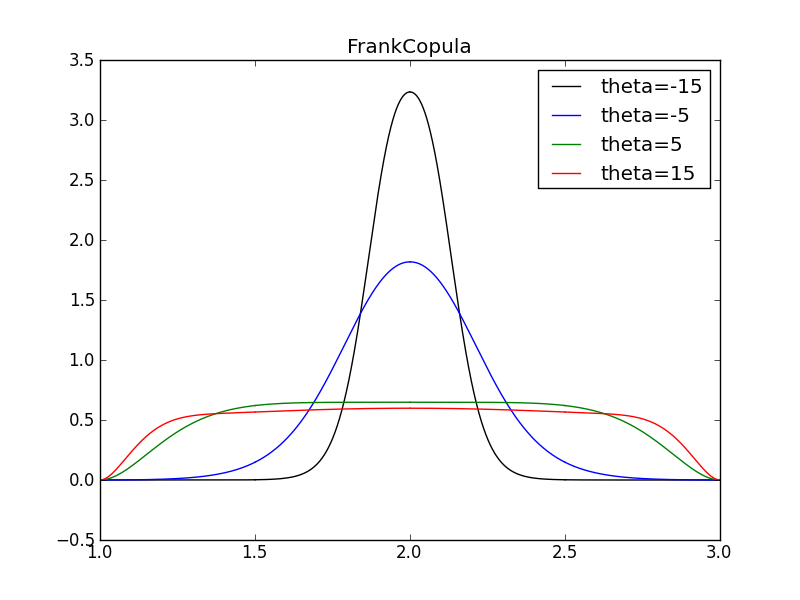
title("FrankCopula")
for i, theta in enumerate([-15, -5, 5, 15]):
print "theta=", theta
ci = FrankCopula(marginals=[X, Y], theta=theta)
Mi = TwoVarsModel(ci, U)
funi = Mi.eval()
funi.plot(label = "theta={0}".format(theta), color = colors[i])
funi.summary()
|
||
|
.
|
||
theta= -15
============= summary =============
PDISTR(1.0,3.0)
mean = 2.0000000000000018
var = 0.014252846375995413
skewness = -4.9561165338666605e-14
kurtosis = 3.1026770429169201
entropy = -0.70732953618959726
median = 2.0
mode = 1.9999999662226453
medianad = 0.08159211759527814
iqrange(0.025) = 0.4631399525971742
ci(0.05) = (1.7684300237014112, 2.2315699762985854)
range = (1.0, 3.0)
tailexp = (None, None)
int_err = -8.8817841970012523e-16
theta= -5
============= summary =============
PDISTR(1.0,3.0)
mean = 2.0000000000000075
var = 0.050819791699204815
skewness = -1.0092089390902306e-13
kurtosis = 3.2393339859713373
entropy = -0.072110299933113603
median = 2.0
mode = 1.9999999662226453
medianad = 0.1479471275093111
iqrange(0.025) = 0.8947141015719
ci(0.05) = (1.552642949214042, 2.447357050785942)
range = (1.0, 3.0)
tailexp = (None, None)
int_err = -3.9968028886505635e-15
theta= 5
============= summary =============
PDISTR(1.0,3.0)
mean = 1.9999999999993949
var = 0.21584687496736882
skewness = 3.2434231701055022e-12
kurtosis = 1.9435041168803537
entropy = 0.57186445211896797
median = 2.0
mode = 2.0000002471148388
medianad = 0.3865083447697602
iqrange(0.025) = 1.6020867102653753
ci(0.05) = (1.1989566448676232, 2.8010433551329985)
range = (1.0, 3.0)
tailexp = (None, None)
int_err = 2.3570034812792073e-13
theta= 15
============= summary =============
PDISTR(1.0,3.0)
mean = 1.9999999951215526
var = 0.25241381916469757
skewness = 2.1774455345141749e-08
kurtosis = 1.8815335283714438
entropy = 0.62222038390773993
median = 2.0000000000012985
mode = 1.9999999662226453
medianad = 0.4237983767557643
iqrange(0.025) = 1.696379505783155
ci(0.05) = (1.1518102485389006, 2.8481897543220556)
range = (1.0, 3.0)
tailexp = (None, None)
int_err = 1.747190170320323e-09
| ... legend()
show()
|
||
|
.
|
||
| ... figure()
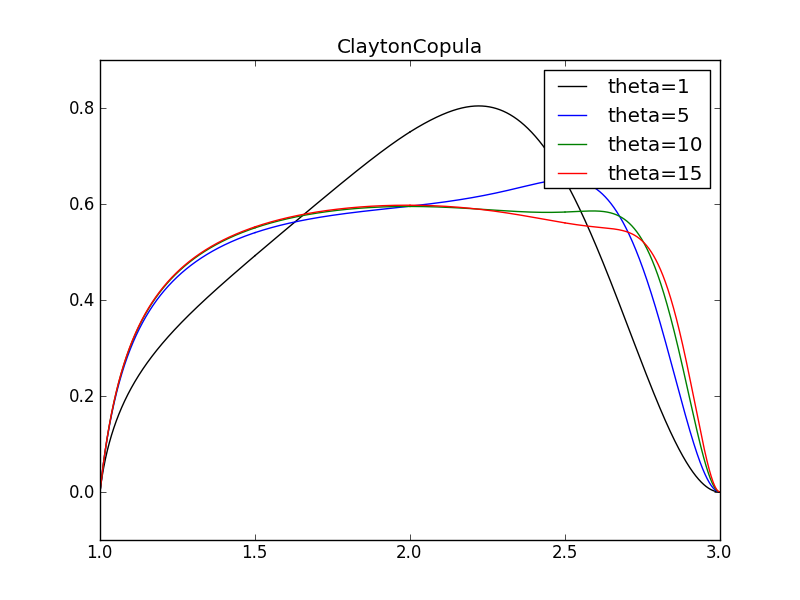
title("ClaytonCopula")
for i, theta in enumerate([1, 5, 10, 15]):
print "theta=", theta
ci = ClaytonCopula(marginals=[X, Y], theta=theta)
Mi = TwoVarsModel(ci, U)
funi = Mi.eval()
funi.plot(label = "theta={0}".format(theta), color = colors[i])
funi.summary()
|
||
|
.
|
||
theta= 1
============= summary =============
PDISTR(1.0,3.0)
mean = 2.0000000000364384
var = 0.19571100819203385
skewness = -0.19611795181203159
kurtosis = 2.1625498665634639
entropy = 0.54717515342304635
median = 2.0337659089824363
mode = 2.2216523787949884
medianad = 0.3389231816727535
iqrange(0.025) = 1.5998146003012104
ci(0.05) = (1.1482688538414556, 2.748083454142666)
range = (1.0, 3.0)
tailexp = (None, None)
int_err = -3.6436631489777938e-11
theta= 5
============= summary =============
PDISTR(1.0,3.0)
mean = 1.9999999969715545
var = 0.24685911350040657
skewness = -0.097077165513144756
kurtosis = 1.9056681466455871
entropy = 0.61769161817013596
median = 2.0189050049787216
mode = 2.5026987825891815
medianad = 0.4170751037475204
iqrange(0.025) = 1.6930481603214609
ci(0.05) = (1.12105142527015, 2.814099585591611)
range = (1.0, 3.0)
tailexp = (None, None)
int_err = 3.0283809904219083e-09
theta= 10
============= summary =============
PDISTR(1.0,3.0)
mean = 1.9999999064219351
var = 0.25623144470808157
skewness = -0.045954201573265144
kurtosis = 1.8963931717206943
entropy = 0.63245970073763291
median = 2.0060883179281133
mode = 1.9966056015039866
medianad = 0.4255026549531106
iqrange(0.025) = 1.7198248313403783
ci(0.05) = (1.119766766359128, 2.8395915976995063)
range = (1.0, 3.0)
tailexp = (None, None)
int_err = 9.356893182488335e-08
theta= 15
============= summary =============
PDISTR(1.0,3.0)
mean = 1.9999998882878809
var = 0.25891506130583752
skewness = -0.026848470676597538
kurtosis = 1.9042006348551108
entropy = 0.63818577466318882
median = 2.002792065433201
mode = 1.9912027379725326
medianad = 0.4253511696443957
iqrange(0.025) = 1.7324335597004805
ci(0.05) = (1.119512057343778, 2.8519456170442585)
range = (1.0, 3.0)
tailexp = (None, None)
int_err = 1.11699159699441e-07
| ... legend()
show()
|
||
|
.
|
||
| ... figure()
Y2 = NormalDistr(sym="Y2")
U2 = X + Y2
U2.setSym("U2")
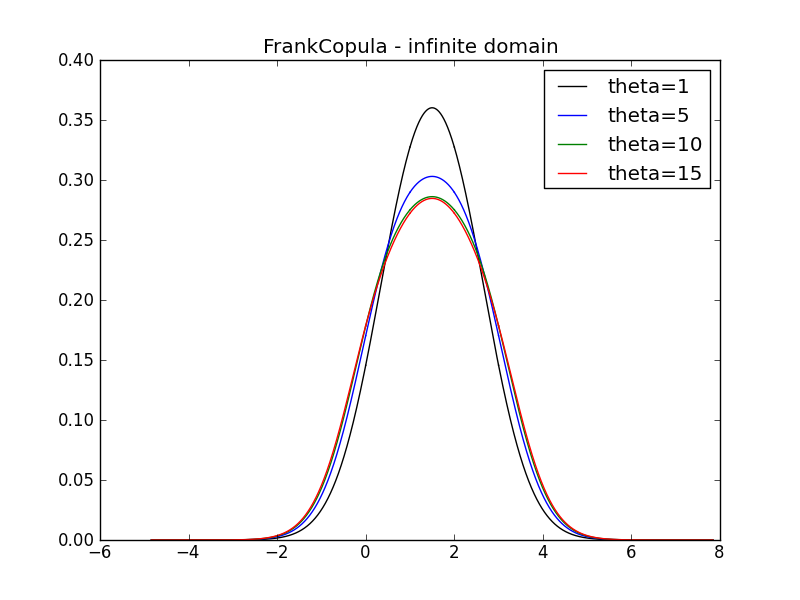
title("FrankCopula - infinite domain")
for i, theta in enumerate([1, 5, 10, 15]):
print "theta=", theta
ci = FrankCopula(marginals=[X, Y2], theta=theta)
Mi = TwoVarsModel(ci, U2)
funi = Mi.eval()
funi.plot(label = "theta={0}".format(theta), color = colors[i])
funi.summary()
|
||
|
.
|
||
theta= 1
============= summary =============
PDISTR(-inf,inf)
mean = 1.4999999999999114
var = 1.1760977653499005
skewness = -3.7120448202495482e-12
kurtosis = 2.9008505150711299
entropy = 1.4997775573826075
median = 1.499999999999926
mode = 1.499999977751401
medianad = 0.743125587270784
iqrange(0.025) = 4.22072217230861
ci(0.05) = (-0.6103610861550173, 3.6103610861535933)
range = (-inf, inf)
tailexp = (0, -206.78393880459012)
int_err = -3.0864200084579352e-14
theta= 5
============= summary =============
PDISTR(-inf,inf)
mean = 1.5000000000005342
var = 1.4442688475770611
skewness = 2.9031894898386142e-11
kurtosis = 2.6561178387832109
entropy = 1.5986951947623518
median = 1.5000000000010352
mode = 1.4999999777510125
medianad = 0.863588230748861
iqrange(0.025) = 4.570589850460351
ci(0.05) = (-0.7852949252258755, 3.7852949252344756)
range = (-inf, inf)
tailexp = (0, -206.54332568089612)
int_err = 5.2813309281418697e-13
theta= 10
============= summary =============
PDISTR(-inf,inf)
mean = 1.50000000000633
var = 1.5645352643987716
skewness = -6.3340741447622797e-12
kurtosis = 2.5756819079151407
entropy = 1.6362627953803246
median = 1.4999999999999145
mode = 1.5000000000009328
medianad = 0.9129146444021918
iqrange(0.025) = 4.715497372223692
ci(0.05) = (-0.8577486861242801, 3.8577486860994115)
range = (-inf, inf)
tailexp = (0, -206.36363601971664)
int_err = -1.8627321907160876e-12
theta= 15
============= summary =============
PDISTR(-inf,inf)
mean = 1.4999999936196864
var = 1.6036726958254053
skewness = 4.4971850583152206e-09
kurtosis = 2.566386772288419
entropy = 1.648459737468678
median = 1.5000000000026361
mode = 1.5000000220972796
medianad = 0.9232041668621214
iqrange(0.025) = 4.771050663975748
ci(0.05) = (-0.8855253216886823, 3.885525342287066)
range = (-inf, inf)
tailexp = (0, -206.24905431136978)
int_err = 1.7482739700369621e-09
| ... legend()
show()
|
||
|
.
|
||