Examples of distributions with singularities

... from functools import partial from pylab import * from mpl_toolkits.axes_grid.inset_locator import zoomed_inset_axes from mpl_toolkits.axes_grid.inset_locator import mark_inset from pacal import *
		.

Using compiled interpolation routine

... from pacal.distr import demo_distr
		.

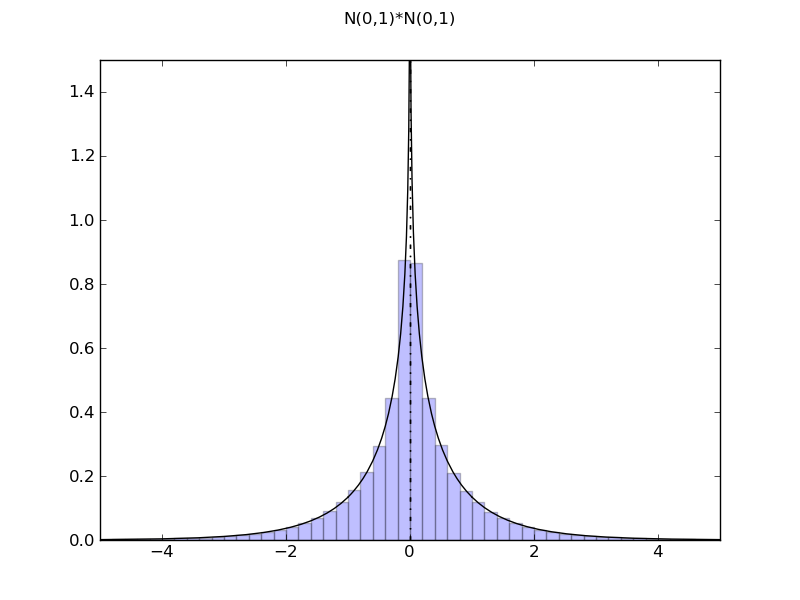
Product of two shifted normal variables

such a product always has a singularity at 0, but the further the factors' means are from zero, the 'lighter' the singularity becomes

... figure() d = NormalDistr(0,1) * NormalDistr(0,1) demo_distr(d, ymax=1.5, xmin=-5, xmax=5)
		.

============= summary =============
  N(0,1)*N(0,1)
                mean  =  5.55111512313e-17
                 std  =  1.0
                 var  =  1.0
             tailexp  =  (-148.1820750072207, -148.1820750072207)
              median  =  0.0
            medianad  =  0.365168011835
      iqrange(0.025)  =  4.36389796793
               range  =  (-inf, inf)
            ci(0.05)  =  (-2.1819489839664534, 2.1819489839664223)
             int_err  =  -8.881784197e-16

... show()
		.

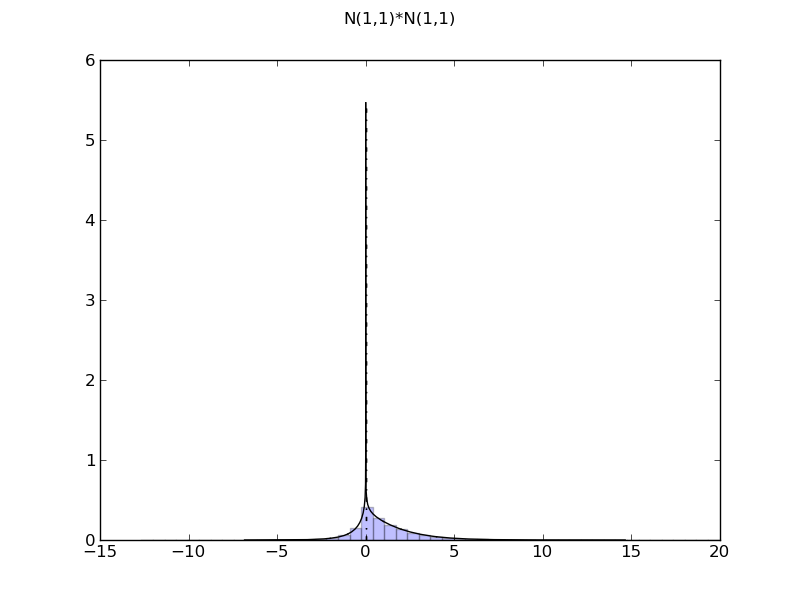
... figure() d = NormalDistr(1,1) * NormalDistr(1,1) demo_distr(d)
		.

============= summary =============
  N(1,1)*N(1,1)
                mean  =  1.0
                 std  =  1.73205080757
                 var  =  3.0
             tailexp  =  (-148.18120012361717, -136.11316051087496)
              median  =  0.608550006303
            medianad  =  0.795218786198
      iqrange(0.025)  =  7.03600471957
               range  =  (-inf, inf)
            ci(0.05)  =  (-1.7253932992908485, 5.3106114202823536)
             int_err  =  -6.66133814775e-16

... show()
		.

... figure() d = NormalDistr(2,1) * NormalDistr(2,1) demo_distr(d)
		.

============= summary =============
  N(2,1)*N(2,1)
                mean  =  4.0
                 std  =  3.0
                 var  =  9.0
             tailexp  =  (-148.17862539773668, -124.04524124537676)
              median  =  3.53736652838
            medianad  =  1.89598902303
      iqrange(0.025)  =  11.4531157325
               range  =  (-inf, inf)
            ci(0.05)  =  (-0.3998570580771057, 11.053258674424656)
             int_err  =  0.0

... show()
		.

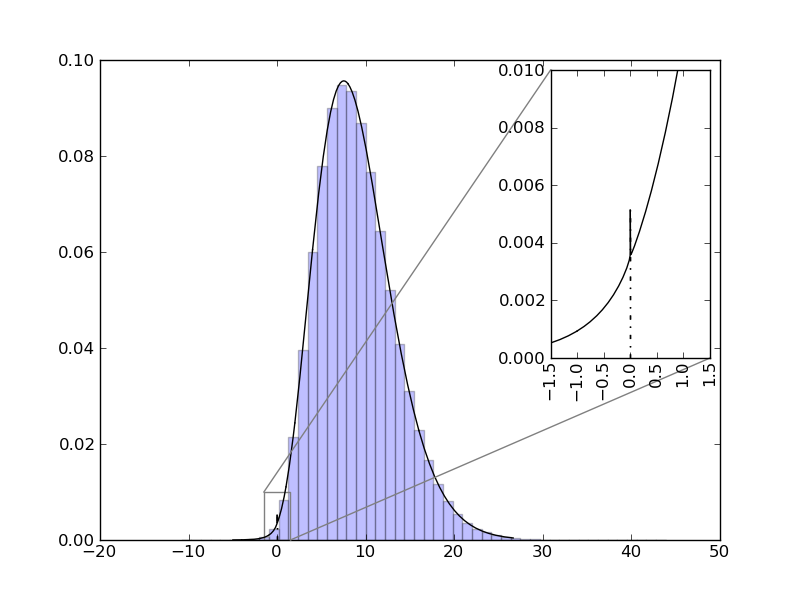
... figure() d = NormalDistr(3,1) * NormalDistr(3,1) d.plot() d.hist() ax=gca() axins = zoomed_inset_axes(ax, 6, loc=1) d.plot(xmin=-1.5, xmax=1.5) axins.set_xlim(-1.5, 1.5) xticks(rotation="vertical") axins.set_ylim(0, 0.01) mark_inset(ax, axins, loc1=2, loc2=4, fc="none", ec="0.5") show()
		.

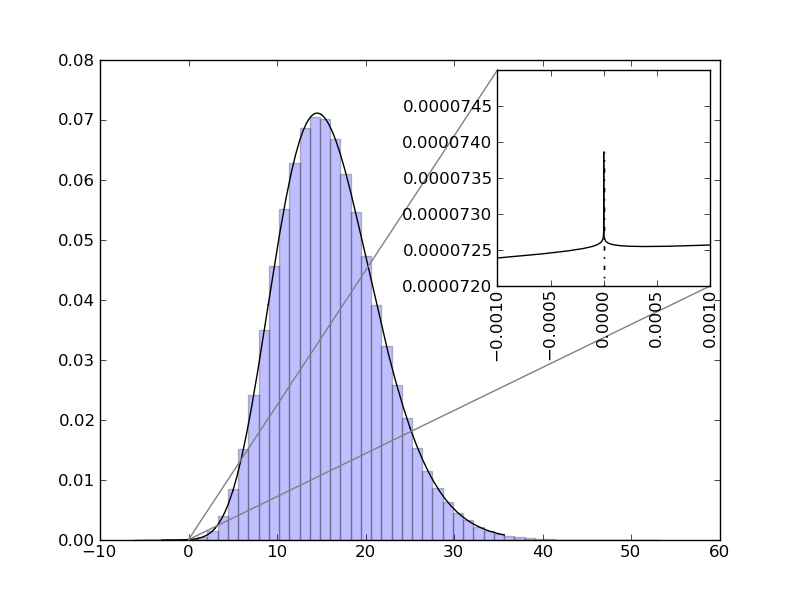
... figure() d = NormalDistr(4,1) * NormalDistr(4,1) d.plot() d.hist() ax=gca() axins = zoomed_inset_axes(ax, 12000, loc=1) d.plot(xmin=-.001, xmax=.001) axins.set_xlim(-.001, .001) xticks(rotation="vertical") axins.set_ylim(0.000072, 0.000075) mark_inset(ax, axins, loc1=2, loc2=4, fc="none", ec="0.5") show()
		.

...
		.

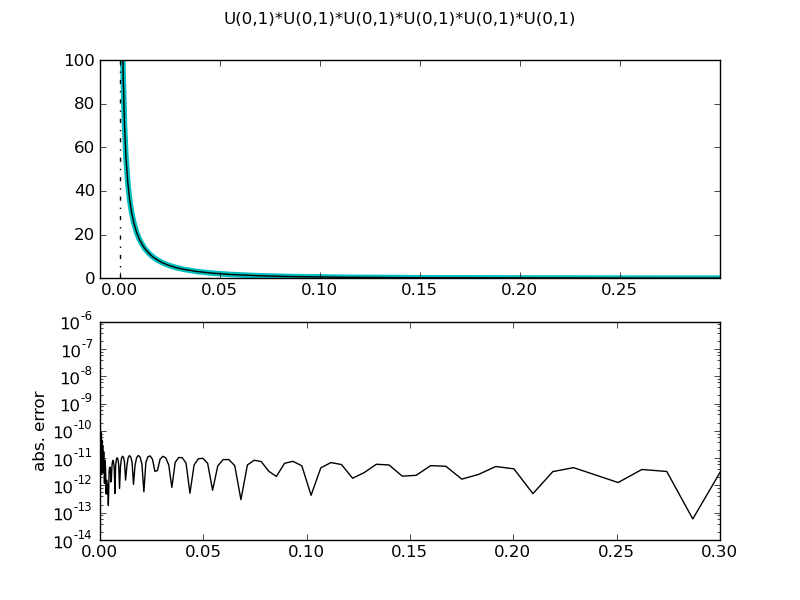
Product of six uniform distributions

... def prod_uni_pdf(n, x): pdf = (-log(x)) ** (n-1) for i in xrange(2, n): pdf /= i return pdf figure() d = UniformDistr(0,1) * UniformDistr(0,1) * UniformDistr(0,1) * UniformDistr(0,1) * UniformDistr(0,1) * UniformDistr(0,1) demo_distr(d, ymax=100, xmin=-0.01, xmax=0.3, theoretical = partial(prod_uni_pdf, 6))
		.

============= summary =============
  U(0,1)*U(0,1)*U(0,1)*U(0,1)*U(0,1)*U(0,1)
                mean  =  0.015625
                 std  =  0.0335797779546
                 var  =  0.00112760148748
             tailexp  =  (None, None)
              median  =  0.00344730956418
            medianad  =  0.003321699878
      iqrange(0.025)  =  0.110584907089
               range  =  (0.0, 1.0)
            ci(0.05)  =  (8.5606702109140504e-06, 0.11059346775905532)
             int_err  =  -4.4408920985e-15
max. abs. error 7.82310962677e-07
max. rel. error 1.42505744692e-10

... show()
		.

...
		.