The Distribution of Linear Regression Coefficients
| ... from pacal import *
|
||
|
.
|
||
Using compiled interpolation routine Compiled sparse grid routine not available
| ... from pylab import figure, show, plot, subplot, title
from scipy.optimize import fmin
from numpy.random import seed
from numpy import concatenate, polyfit, array
seed(1)
import time
t0 = time.time()
params.interpolation_nd.maxq = 7
params.interpolation.maxn = 50
params.interpolation_pole.maxn = 50
params.interpolation_finite.maxn = 50
params.interpolation_infinite.maxn = 50
params.interpolation.debug_info = False
params.interpolation_nd.debug_info = False
params.models.debug_info = True
|
||
|
.
|
||
Sample
| ... n=10
#Xobs = UniformDistr().rand(n)
a, b = 0.3, 0.7
#Ei = NormalDistr(0.0,0.25) | Between(-1,1)
#Yobs = a * Xobs + b + Ei.rand(n)
Xobs=array([ -0.165955990595, 0.440648986884, -0.999771250365, -0.395334854736, -0.706488218366, -0.815322810462, -0.627479577245, -0.308878545914, -0.206465051539, 0.0776334680067 ])
Yobs=array([ 0.599227844272, 0.952772646868, 0.193629370472, 0.872776787585, 0.00800832135878, 0.565696815404, 0.459561157571, 0.644246153468, 0.368440390549, 0.511201707273 ])
print '{0:{align}15}\t{0:{align}15}'.format("Xobs","Xobs", align = '>')
|
||
|
.
|
||
Xobs Xobs
| ... for i in range(len(Xobs)):
print '{0:{align}20}\t{0:{align}14}'.format(Xobs[i], Yobs[i], align = '>')
|
||
|
.
|
||
-0.165955990595 0.599227844272 0.440648986884 0.952772646868 -0.999771250365 0.193629370472 -0.395334854736 0.872776787585 -0.706488218366 0.00800832135878 -0.815322810462 0.565696815404 -0.627479577245 0.459561157571 -0.308878545914 0.644246153468 -0.206465051539 0.368440390549 0.0776334680067 0.511201707273
| ... print "x=c(", ", ".join(str(x) for x in Xobs), ")"
|
||
|
.
|
||
x=c( -0.165955990595, 0.440648986884, -0.999771250365, -0.395334854736, -0.706488218366, -0.815322810462, -0.627479577245, -0.308878545914, -0.206465051539, 0.0776334680067 )
| ... print "y=c(", ", ".join(str(x) for x in Yobs), ")"
|
||
|
.
|
||
y=c( 0.599227844272, 0.952772646868, 0.193629370472, 0.872776787585, 0.00800832135878, 0.565696815404, 0.459561157571, 0.644246153468, 0.368440390549, 0.511201707273 )
Model
| ... X = []
E = []
Y = []
#A = UniformDistr(0,1, sym = "A")
A = UniformDistr(-0.5, 1.5, sym = "A")
B = UniformDistr(-0.0, 1.5, sym = "B")
#A = NormalDistr(0.0,0.2) | Between(-1,1)
#B = NormalDistr(0.0,0.2) | Between(-1,1)
for i in range(n):
X.append(UniformDistr(-1, 1, sym = "X{0}".format(i)))
E.append(NormalDistr(0.0,0.2) | Between(-1.0,1.0))
E[i].setSym("E{0}".format(i))
Y.append(A * X[i] + B + E[i])
Y[i].setSym("Y{0}".format(i))
M = Model(X + E + [A, B], Y)
M.toGraphwiz(f=open('bn.dot', mode="w+"))
print M
|
||
|
.
|
||
Model: free_vars: A ~ U(-0.5,1.5) B ~ U(-0.0,1.5) E0 ~ N(0.0,0.2) | X>-1.0 | X<1.0 E1 ~ N(0.0,0.2) | X>-1.0 | X<1.0 E2 ~ N(0.0,0.2) | X>-1.0 | X<1.0 E3 ~ N(0.0,0.2) | X>-1.0 | X<1.0 E4 ~ N(0.0,0.2) | X>-1.0 | X<1.0 E5 ~ N(0.0,0.2) | X>-1.0 | X<1.0 E6 ~ N(0.0,0.2) | X>-1.0 | X<1.0 E7 ~ N(0.0,0.2) | X>-1.0 | X<1.0 E8 ~ N(0.0,0.2) | X>-1.0 | X<1.0 E9 ~ N(0.0,0.2) | X>-1.0 | X<1.0 X0 ~ U(-1,1) X1 ~ U(-1,1) X2 ~ U(-1,1) X3 ~ U(-1,1) X4 ~ U(-1,1) X5 ~ U(-1,1) X6 ~ U(-1,1) X7 ~ U(-1,1) X8 ~ U(-1,1) X9 ~ U(-1,1) dep vars: X61312592(2), X61359024(2), X61361616(2), X61735696(2), X61761008(2), X61761424(2), X61788080(2), X61820848(2), X61849264(2), X61872944(2), X61358160(11), Y0(11), Y1(11), X61361424(11), X61374192(11), Y2(11), Y3(11), X61737808(11), Y4(11), X61762960(11), X61786384(11), Y5(11), Y6(11), X61819760(11), Y7(11), X61848176(11), Y8(11), X61872752(11), X61899920(11), Y9(11) Equations: X61358160 = B + X61312592(11) X61786384 = B + X61761424(11) Y0 = E0 + X61358160(11) Y5 = E5 + X61786384(11) Y3 = E3 + X61737808(11) Y6 = E6 + X61819760(11) X61848176 = B + X61820848(11) Y8 = E8 + X61872752(11) X61735696 = A*X3(2) X61872944 = A*X9(2) X61737808 = B + X61735696(11) X61819760 = B + X61788080(11) Y1 = E1 + X61361424(11) X61359024 = A*X1(2) X61361424 = B + X61359024(11) Y7 = E7 + X61848176(11) Y4 = E4 + X61762960(11) X61899920 = B + X61872944(11) Y9 = E9 + X61899920(11) X61762960 = B + X61761008(11) X61361616 = A*X2(2) X61761008 = A*X4(2) X61820848 = A*X7(2) X61312592 = A*X0(2) X61849264 = A*X8(2) X61374192 = B + X61361616(11) Y2 = E2 + X61374192(11) X61761424 = A*X5(2) X61872752 = B + X61849264(11) X61788080 = A*X6(2) Factors: F_0 (X0)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_1 (X1)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_2 (X2)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_3 (X3)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_4 (X4)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_5 (X5)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_6 (X6)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_7 (X7)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_8 (X8)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_9 (X9)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_10 (E0)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_11 (E1)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_12 (E2)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_13 (E3)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_14 (E4)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_15 (E5)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_16 (E6)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_17 (E7)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_18 (E8)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_19 (E9)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_20 (A)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_21 (B)<class 'pacal.depvars.nddistr.Factor1DDistr'>
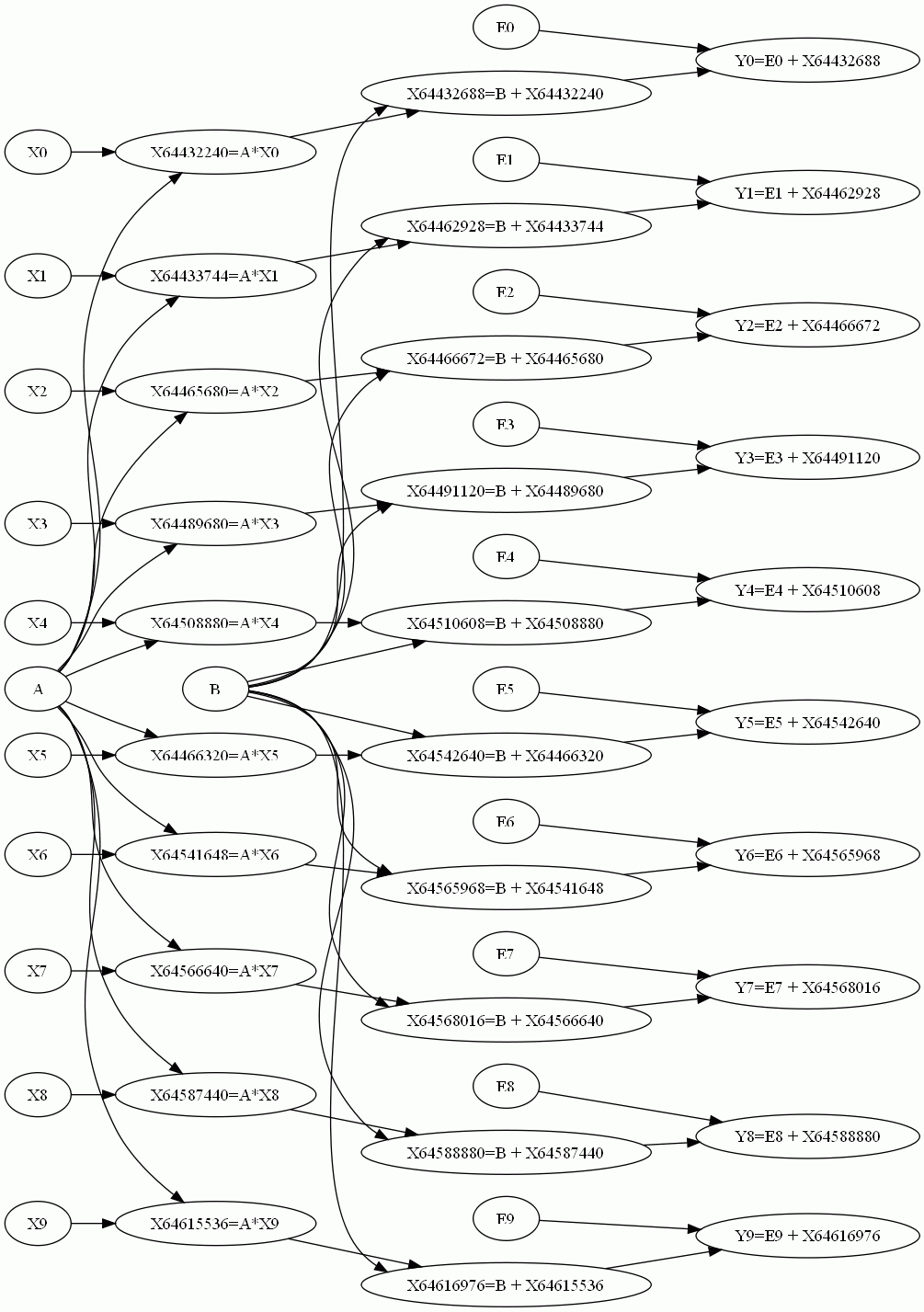
Inference
| ... MAB = M.inference([A,B], X + Y, concatenate((Xobs, Yobs)))
|
||
|
.
|
||
condition on variable: X0 = -0.165955990595 condition on variable: X1 = 0.440648986884 condition on variable: X2 = -0.999771250365 condition on variable: X3 = -0.395334854736 condition on variable: X4 = -0.706488218366 condition on variable: X5 = -0.815322810462 condition on variable: X6 = -0.627479577245 condition on variable: X7 = -0.308878545914 condition on variable: X8 = -0.206465051539 condition on variable: X9 = 0.0776334680067 exchange free variable: A with dependent variable X61312592 exchange free variable: X61312592 with dependent variable X61359024 exchange free variable: X61359024 with dependent variable X61361616 exchange free variable: X61361616 with dependent variable X61735696 exchange free variable: X61735696 with dependent variable X61761008 exchange free variable: X61761008 with dependent variable X61761424 exchange free variable: X61761424 with dependent variable X61788080 exchange free variable: X61788080 with dependent variable X61820848 exchange free variable: X61820848 with dependent variable X61849264 exchange free variable: X61849264 with dependent variable X61872944 exchange free variable: B with dependent variable X61358160 exchange free variable: E0 with dependent variable Y0 condition on variable: Y0 = 0.599227844272 exchange free variable: X61358160 with dependent variable X61361424 exchange free variable: E1 with dependent variable Y1 condition on variable: Y1 = 0.952772646868 exchange free variable: X61361424 with dependent variable X61374192 exchange free variable: E2 with dependent variable Y2 condition on variable: Y2 = 0.193629370472 exchange free variable: X61374192 with dependent variable X61737808 exchange free variable: E3 with dependent variable Y3 condition on variable: Y3 = 0.872776787585 exchange free variable: X61737808 with dependent variable X61762960 exchange free variable: E4 with dependent variable Y4 condition on variable: Y4 = 0.00800832135878 exchange free variable: X61762960 with dependent variable X61786384 exchange free variable: E5 with dependent variable Y5 condition on variable: Y5 = 0.565696815404 exchange free variable: X61786384 with dependent variable X61819760 exchange free variable: E6 with dependent variable Y6 condition on variable: Y6 = 0.459561157571 exchange free variable: X61819760 with dependent variable X61848176 exchange free variable: E7 with dependent variable Y7 condition on variable: Y7 = 0.644246153468 exchange free variable: X61848176 with dependent variable X61872752 exchange free variable: E8 with dependent variable Y8 condition on variable: Y8 = 0.368440390549 exchange free variable: X61872752 with dependent variable X61899920 exchange free variable: E9 with dependent variable Y9 condition on variable: Y9 = 0.511201707273 exchange free variable: X61872944 with dependent variable A exchange free variable: X61899920 with dependent variable B
| ... params.interpolation.maxn = 100
params.interpolation_pole.maxn = 100
MA = MAB.inference([A],[],[])
MB = MAB.inference([B],[],[])
print MAB
|
||
|
.
|
||
Model: free_vars: A ~ U(-0.5,1.5) B ~ U(-0.0,1.5) dep vars: Equations: Factors: F_0 (A)<class 'pacal.depvars.nddistr.NDDistrWithVarSubst'> F_1 (B,A)<class 'pacal.depvars.nddistr.NDDistrWithVarSubst'> F_2 (B,A)<class 'pacal.depvars.nddistr.NDDistrWithVarSubst'> F_3 (B,A)<class 'pacal.depvars.nddistr.NDDistrWithVarSubst'> F_4 (B,A)<class 'pacal.depvars.nddistr.NDDistrWithVarSubst'> F_5 (B,A)<class 'pacal.depvars.nddistr.NDDistrWithVarSubst'> F_6 (B,A)<class 'pacal.depvars.nddistr.NDDistrWithVarSubst'> F_7 (B,A)<class 'pacal.depvars.nddistr.NDDistrWithVarSubst'> F_8 (B,A)<class 'pacal.depvars.nddistr.NDDistrWithVarSubst'> F_9 (B,A)<class 'pacal.depvars.nddistr.NDDistrWithVarSubst'> F_10 (B,A)<class 'pacal.depvars.nddistr.NDDistrWithVarSubst'> F_11 (B,A)<class 'pacal.depvars.nddistr.NDDistrWithVarSubst'> F_12 ()<class 'pacal.depvars.nddistr.NDConstFactor'>
| ... print MA
|
||
|
.
|
||
Model: free_vars: A ~ U(-0.5,1.5) dep vars: Equations: Factors: F_0 (A)<class 'pacal.depvars.nddistr.NDDistrWithVarSubst'> F_1 (A)<class 'pacal.depvars.nddistr.NDInterpolatedDistr'> F_2 ()<class 'pacal.depvars.nddistr.NDConstFactor'>
| ... print MB
|
||
|
.
|
||
Model: free_vars: B ~ U(-0.0,1.5) dep vars: Equations: Factors: F_0 (B)<class 'pacal.depvars.nddistr.NDInterpolatedDistr'> F_1 ()<class 'pacal.depvars.nddistr.NDConstFactor'>
| ... figure(1)
MAB.plot(have_3d=True)
title("Joint distribution of A and B conditioned on sample")
show()
|
||
|
.
|
||
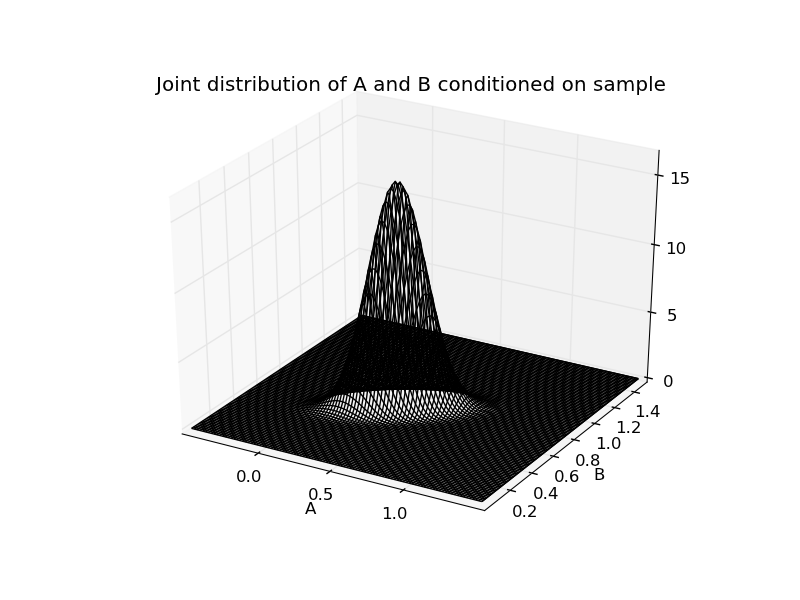
| ... figure(2)
MAB.plot(have_3d=False, cont_levels=10)
title("Joint distribution of A and B conditioned on sample")
show()
|
||
|
.
|
||
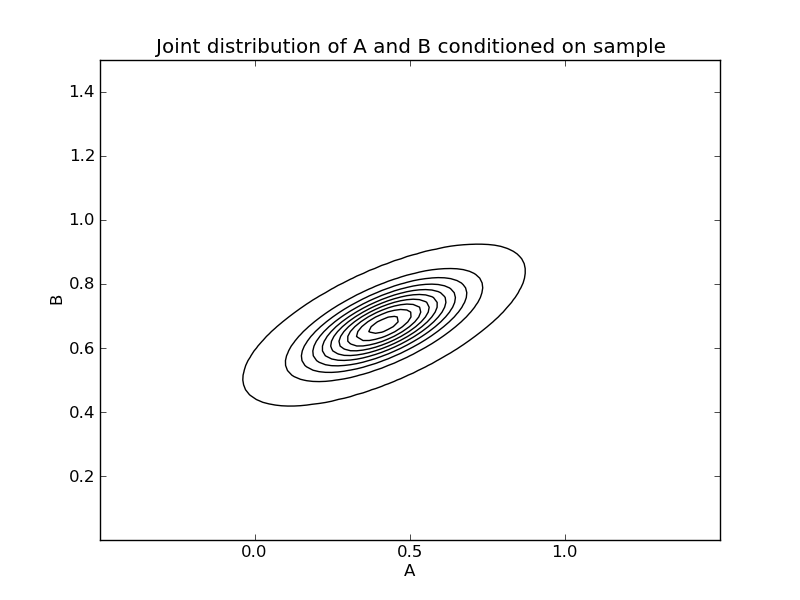
| ... figure(3)
subplot(211)
MA.plot()
|
||
|
.
|
||
============= summary =============
FUN(-0.5,1.5)
mean = 0.41645355509034099
var = 0.023464241392269252
skewness = -3.7665393628279955e-08
kurtosis = 2.9999985597715617
entropy = -0.45720036463886982
median = 0.4164535332421927
mode = 0.41645353919269024
medianad = 0.10331862001613233
iqrange(0.025) = 0.6004561331294082
ci(0.05) = (0.11622542905463824, 0.7166815621840464)
range = (-0.5, 1.5)
tailexp = (None, None)
int_err = -3.4207779275874373e-08
| ... title("Marginalized distribution of A")
subplot(212)
MB.plot()
|
||
|
.
|
||
============= summary =============
FUN(-0,1.5)
mean = 0.67195270604723933
var = 0.0072251407656638185
skewness = -7.8840675802035367e-07
kurtosis = 2.9999995867207456
entropy = -1.0461558406701483
median = 0.6719526773756899
mode = 0.67195268094315619
medianad = 0.057332184251915205
iqrange(0.025) = 0.33319706834906826
ci(0.05) = (0.5053541212593485, 0.8385511896084168)
range = (-0, 1.5)
tailexp = (None, None)
int_err = -3.6473167597250722e-08
| ... title("Marginalized distribution of B")
show()
|
||
|
.
|
||
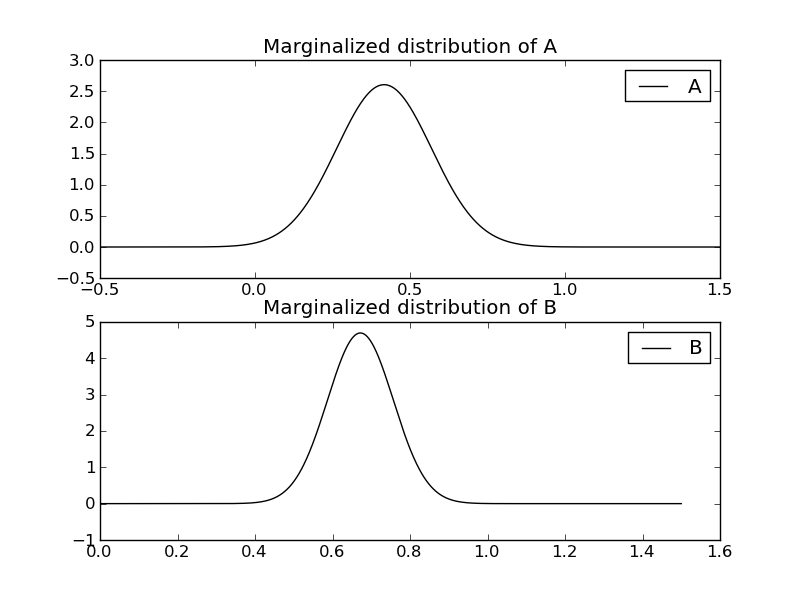
Estimation of coefficients
| ... print "original coefficients a=", a, "b=", b
|
||
|
.
|
||
original coefficients a= 0.3 b= 0.7
| ... print "mean est. A=", MA.as1DDistr().mean(), "est. B=", MB.as1DDistr().mean()
|
||
|
.
|
||
mean est. A= 0.41645355509 est. B= 0.671952706047
| ... print "median est. A=", MA.as1DDistr().median(), "est. B=", MB.as1DDistr().median()
|
||
|
.
|
||
median est. A= 0.416453533242 est. B= 0.671952677376
| ... print "mode est. A=", MA.as1DDistr().mode(), "est. B=", MB.as1DDistr().mode()
|
||
|
.
|
||
mode est. A= 0.416453539193 est. B= 0.671952680943
| ... print MA.as1DDistr().cdf(0.0)
|
||
|
.
|
||
0.00327682546711
| ... print MB.as1DDistr().cdf(0.0)
|
||
|
.
|
||
0.0
| ... MAB.nddistr(1, 3)
abopt = MAB.nddistr.mode()
|
||
|
.
|
||
Warning: Desired error not necessarily achieved due to precision loss
Current function value: -16.428083
Iterations: 31
Function evaluations: 2291
Gradient evaluations: 524
| ... (ar,br)=polyfit(Xobs,Yobs,1)
|
||
|
.
|
||
Least squares estimates are maximum log-likelihood estimates (are equal to maximum a posteriori in this case, because of uniform a priori distribution of coefficients)
| ... print " MAP a=", abopt[0], "b=", abopt[1]
|
||
|
.
|
||
MAP a= 0.416453467936 b= 0.671952615709
| ... print "polyfit (LSE) est. a=", ar, "b=", br
|
||
|
.
|
||
polyfit (LSE) est. a= 0.416453539158 b= 0.671952681142
| ... print "computation time=", time.time() - t0
|
||
|
.
|
||
computation time= 154.951999903
| ... |
||
|
.
|
||