Simple differential equation
| ... from pacal import *
|
||
|
.
|
||
Using compiled interpolation routine Compiled sparse grid routine not available
| ... from pylab import figure, show, subplot, title, plot, xlabel, ylabel, legend, rc
from matplotlib.lines import Line2D
rc('axes', labelsize=18)
rc('xtick', labelsize=15.0)
rc('ytick', labelsize=15.0)
rc('legend', fontsize=17.0)
linestyles = ["-", "--", "-.", ":"]
pfargs = {"linewidth":3, "color":"k", "dash_joinstyle":"round"}
from pacal.depvars.models import Model
from pacal.depvars.nddistr import NDProductDistr, Factor1DDistr
from numpy import array, zeros
import time
t0 = time.time()
params.interpolation_nd.maxq = 7
params.interpolation.maxn = 100
params.interpolation_pole.maxn =100
params.interpolation_nd.debug_info = False
params.models.debug_info = False
|
||
|
.
|
||
Euler's method applied to equation y'(t) = ay(t) + u(t). Noisy observation o of the state y are available.
After discretization:
Y(i) = Y[i-1] + h * A * Y(i-1) + h * U[i-1]
O(i) = Y(i) + E(i), i=1,...,n
| ... A = BetaDistr(3, 3, sym="A") # parameter of equation
Y0 = BetaDistr(3, 3, sym="Y0") # initial value
n = 10 # number time points
h = 1.0 / n
K = (1 + h * A)
K.setSym("K")
Y, O, E, U = [], [], [], [] # lists of states, observations and errors
# U's will be conditioned on, to treat them as constants
for i in xrange(n):
#Y.append(Y[i] * K)
#Y[i + 1].setSym("Y" + str(i + 1))
U.append(UniformDistr(-0.1,0.1, sym="U{0}".format(i)))
if i==0:
Y.append(Y0 * K+ h*U[i])
else:
Y.append(Y[i-1] * K+ h*U[i])
Y[-1].setSym("Y" + str(i+1))
ei = NormalDistr(0.0, 0.1) | Between(-0.4, 0.4)
ei.setSym("E{0}".format(i))
E.append(ei)
O.append(Y[-1] + E[-1])
O[-1].setSym("O{0}".format(i))
|
||
|
.
|
||
Warning: arguments treated as independent Warning: arguments treated as independent Warning: arguments treated as independent Warning: arguments treated as independent Warning: arguments treated as independent Warning: arguments treated as independent Warning: arguments treated as independent Warning: arguments treated as independent Warning: arguments treated as independent
Model
| ... P = NDProductDistr([A, Y0] + E + U)
M = Model(P, O)
print M
|
||
|
.
|
||
Model: free_vars: A ~ Beta(3,3) E0 ~ N(0.0,0.1) | X>-0.4 | X<0.4 E1 ~ N(0.0,0.1) | X>-0.4 | X<0.4 E2 ~ N(0.0,0.1) | X>-0.4 | X<0.4 E3 ~ N(0.0,0.1) | X>-0.4 | X<0.4 E4 ~ N(0.0,0.1) | X>-0.4 | X<0.4 E5 ~ N(0.0,0.1) | X>-0.4 | X<0.4 E6 ~ N(0.0,0.1) | X>-0.4 | X<0.4 E7 ~ N(0.0,0.1) | X>-0.4 | X<0.4 E8 ~ N(0.0,0.1) | X>-0.4 | X<0.4 E9 ~ N(0.0,0.1) | X>-0.4 | X<0.4 U0 ~ U(-0.1,0.1) U1 ~ U(-0.1,0.1) U2 ~ U(-0.1,0.1) U3 ~ U(-0.1,0.1) U4 ~ U(-0.1,0.1) U5 ~ U(-0.1,0.1) U6 ~ U(-0.1,0.1) U7 ~ U(-0.1,0.1) U8 ~ U(-0.1,0.1) U9 ~ U(-0.1,0.1) Y0 ~ Beta(3,3) dep vars: X66437744(11), X66438288(20), X66438800(20), X66439312(20), X66439824(20), X66440336(20), X66440848(20), X66461872(20), X66462384(20), X66462896(20), X66437168(1), K(10), X66437808(1), X66438352(1), X66438864(1), X66439376(1), X66439888(1), X66440400(1), X66440912(1), X66461936(1), X66462448(1), X66462960(1), Y1(20), O0(11), Y2(20), O1(11), Y3(20), O2(11), Y4(20), O3(11), Y5(20), O4(11), Y6(20), O5(11), Y7(20), O6(11), Y8(20), O7(11), Y9(20), O8(11), Y10(20), O9(11) Equations: X66437808 = 0.1*U0(1) K = 1 + X66437168(10) X66439312 = K*Y3(20) X66461872 = K*Y7(20) X66439376 = 0.1*U3(1) X66461936 = 0.1*U7(1) Y4 = X66439312 + X66439376(20) X66437168 = 0.1*A(1) O5 = E5 + Y6(11) Y1 = X66437744 + X66437808(20) O7 = E7 + Y8(11) O3 = E3 + Y4(11) X66437744 = K*Y0(11) X66439824 = K*Y4(20) X66462384 = K*Y8(20) X66439888 = 0.1*U4(1) Y9 = X66462384 + X66462448(20) X66462448 = 0.1*U8(1) Y5 = X66439824 + X66439888(20) X66440912 = 0.1*U6(1) X66440336 = K*Y5(20) O0 = E0 + Y1(11) O8 = E8 + Y9(11) X66438288 = K*Y1(20) X66462896 = K*Y9(20) X66438352 = 0.1*U1(1) X66462960 = 0.1*U9(1) Y2 = X66438288 + X66438352(20) Y10 = X66462896 + X66462960(20) O6 = E6 + Y7(11) O1 = E1 + Y2(11) O9 = E9 + Y10(11) O4 = E4 + Y5(11) Y6 = X66440336 + X66440400(20) X66438800 = K*Y2(20) Y7 = X66440848 + X66440912(20) X66438864 = 0.1*U2(1) Y3 = X66438800 + X66438864(20) X66440400 = 0.1*U5(1) Y8 = X66461872 + X66461936(20) X66440848 = K*Y6(20) O2 = E2 + Y3(11) Factors: F_0 (A)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_1 (Y0)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_2 (E0)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_3 (E1)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_4 (E2)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_5 (E3)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_6 (E4)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_7 (E5)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_8 (E6)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_9 (E7)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_10 (E8)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_11 (E9)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_12 (U0)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_13 (U1)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_14 (U2)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_15 (U3)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_16 (U4)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_17 (U5)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_18 (U6)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_19 (U7)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_20 (U8)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_21 (U9)<class 'pacal.depvars.nddistr.Factor1DDistr'>
| ... M.eliminate_other(E + Y + O + [A, Y0] + U)
print M
|
||
|
.
|
||
Model: free_vars: A ~ Beta(3,3) E0 ~ N(0.0,0.1) | X>-0.4 | X<0.4 E1 ~ N(0.0,0.1) | X>-0.4 | X<0.4 E2 ~ N(0.0,0.1) | X>-0.4 | X<0.4 E3 ~ N(0.0,0.1) | X>-0.4 | X<0.4 E4 ~ N(0.0,0.1) | X>-0.4 | X<0.4 E5 ~ N(0.0,0.1) | X>-0.4 | X<0.4 E6 ~ N(0.0,0.1) | X>-0.4 | X<0.4 E7 ~ N(0.0,0.1) | X>-0.4 | X<0.4 E8 ~ N(0.0,0.1) | X>-0.4 | X<0.4 E9 ~ N(0.0,0.1) | X>-0.4 | X<0.4 U0 ~ U(-0.1,0.1) U1 ~ U(-0.1,0.1) U2 ~ U(-0.1,0.1) U3 ~ U(-0.1,0.1) U4 ~ U(-0.1,0.1) U5 ~ U(-0.1,0.1) U6 ~ U(-0.1,0.1) U7 ~ U(-0.1,0.1) U8 ~ U(-0.1,0.1) U9 ~ U(-0.1,0.1) Y0 ~ Beta(3,3) dep vars: Y1(3), O0(11), Y2(12), O1(11), Y3(12), O2(11), Y4(12), O3(11), Y5(12), O4(11), Y6(12), O5(11), Y7(12), O6(11), Y8(12), O7(11), Y9(12), O8(11), Y10(12), O9(11) Equations: Y4 = 0.1*U3 + Y3*(1 + 0.1*A)(12) O5 = E5 + Y6(11) Y1 = 0.1*U0 + Y0*(1 + 0.1*A)(3) O7 = E7 + Y8(11) O3 = E3 + Y4(11) Y9 = 0.1*U8 + Y8*(1 + 0.1*A)(12) Y5 = 0.1*U4 + Y4*(1 + 0.1*A)(12) O0 = E0 + Y1(11) O8 = E8 + Y9(11) Y2 = 0.1*U1 + Y1*(1 + 0.1*A)(12) Y10 = 0.1*U9 + Y9*(1 + 0.1*A)(12) O6 = E6 + Y7(11) O1 = E1 + Y2(11) O9 = E9 + Y10(11) O4 = E4 + Y5(11) Y6 = 0.1*U5 + Y5*(1 + 0.1*A)(12) Y7 = 0.1*U6 + Y6*(1 + 0.1*A)(12) Y3 = 0.1*U2 + Y2*(1 + 0.1*A)(12) Y8 = 0.1*U7 + Y7*(1 + 0.1*A)(12) O2 = E2 + Y3(11) Factors: F_0 (A)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_1 (Y0)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_2 (E0)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_3 (E1)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_4 (E2)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_5 (E3)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_6 (E4)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_7 (E5)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_8 (E6)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_9 (E7)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_10 (E8)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_11 (E9)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_12 (U0)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_13 (U1)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_14 (U2)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_15 (U3)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_16 (U4)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_17 (U5)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_18 (U6)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_19 (U7)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_20 (U8)<class 'pacal.depvars.nddistr.Factor1DDistr'> F_21 (U9)<class 'pacal.depvars.nddistr.Factor1DDistr'>
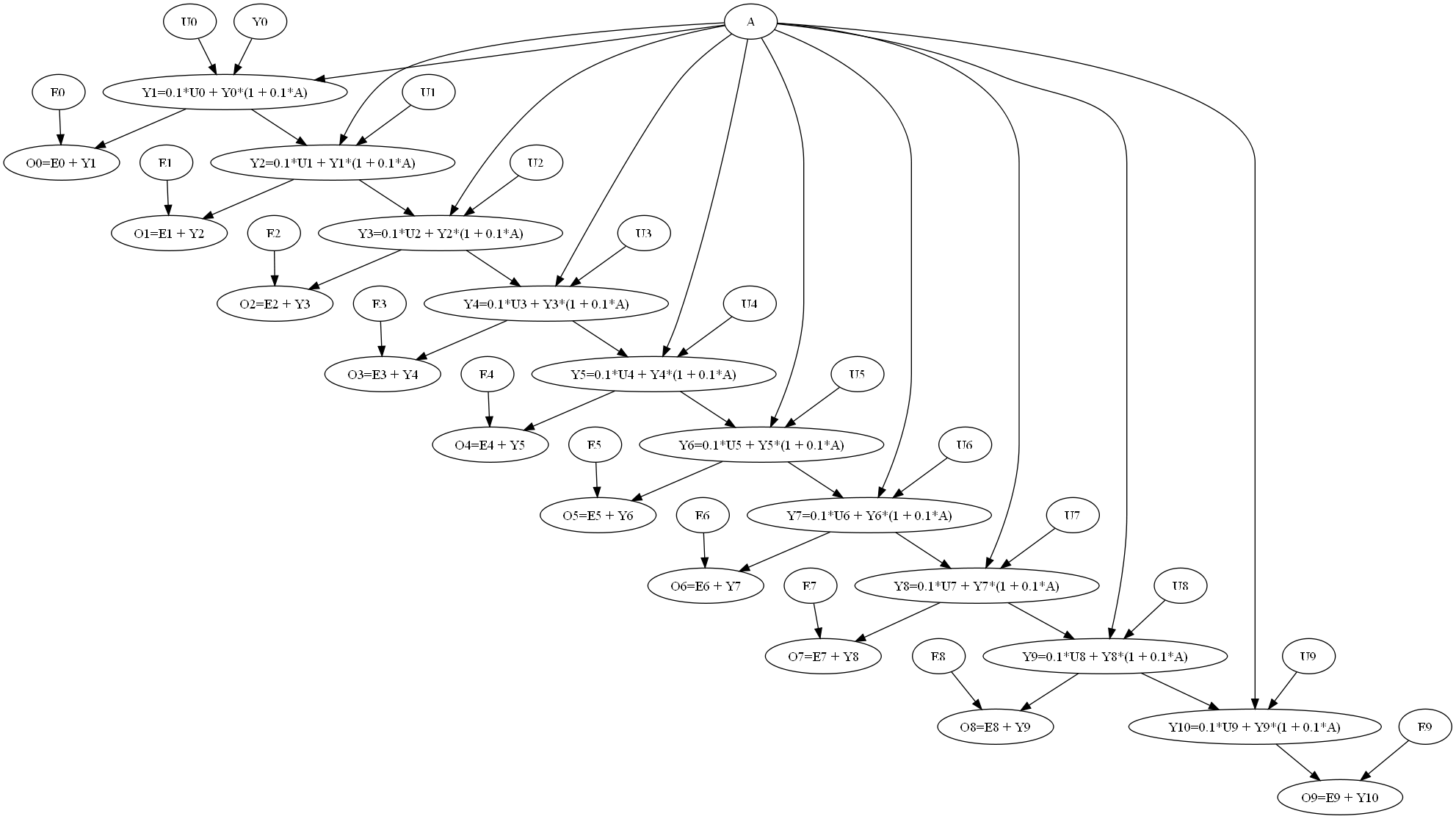
| ... M.toGraphwiz(f=open('bn.dot', mode="w+"))
|
||
|
.
|
||
Joint distribution of initial condition and the parameter of the equation
| ... i = 0
ay0 = []
ui = [0.0]*n
figure()
for yend in [0.25, 1.25, 2.25]:
M2 = M.inference(wanted_rvs=[A, Y0], cond_rvs=[O[-1]] + U, cond_X=[yend] + ui)
subplot(1, 3, i + 1)
title("O_{0}={1}".format(n, yend))
M2.plot()
ay0.append(M2.nddistr.mode()) # "most probable" state
print "yend=", yend, ", MAP est. of A, Y0 =", ay0[i]
i += 1
|
||
|
.
|
||
Current function value: -13.280050
Iterations: 65
Function evaluations: 3408
Gradient evaluations: 754
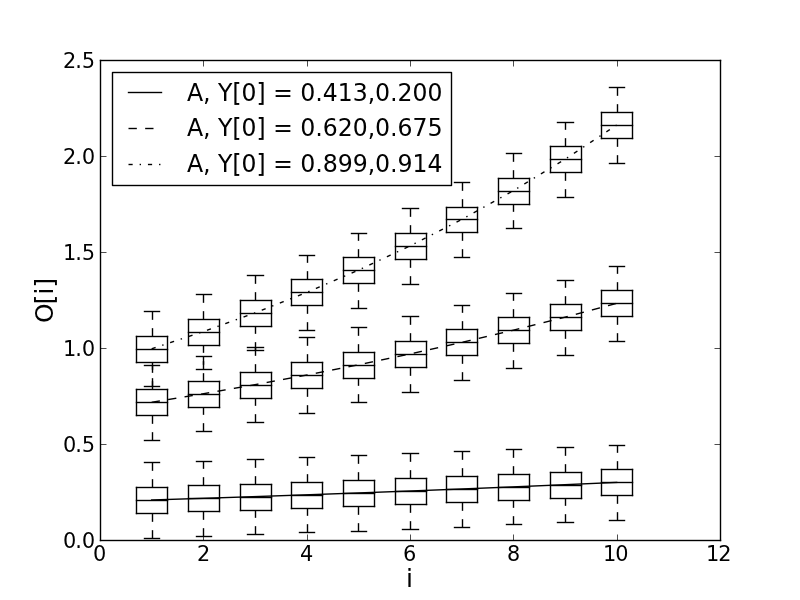
yend= 0.25 , MAP est. of A, Y0 = [0.412742895461 0.200191315344]
Current function value: -18.457584
Iterations: 37
Function evaluations: 2421
Gradient evaluations: 565
yend= 1.25 , MAP est. of A, Y0 = [0.619901146383 0.675411442956]
Current function value: -97.064033
Iterations: 400
Function evaluations: 16320
Gradient evaluations: 3532
yend= 2.25 , MAP est. of A, Y0 = [0.899092946994 0.913707881827]
| ... show()
|
||
|
.
|
||

Trajectories
| ... figure()
styles=['-', '--', '-.', ':']
for j in range(len(ay0)):
ymean, ystd = [], []
for i in range(n):
Myi = M.inference([O[i]], [A, Y0] + U, list(ay0[j]) + ui).as1DDistr()
ymean.append(Myi.mean())
ystd.append(Myi.std())
Myi.boxplot(pos=i+1, useci=0.05, showMean=False)
plot(range(1, n+1, 1), ymean, 'k', linestyle=styles[j], label="A, Y[0] = {0:.3f},{1:.3f}".format(*ay0[j]))
ylabel("O[i]")
xlabel("i")
legend(loc='upper left')
show()
|
||
|
.
|
||
| ... print "computation time=", time.time() - t0
|
||
|
.
|
||
computation time= 211.868999958
| ... |
||
|
.
|
||