CHAPTERS 6, 7, 8
| ... from functools import partial
import numpy
from pylab import figure, show
from pacal import *
|
||
|
.
|
||
Using compiled interpolation routine
| ... from pacal.distr import demo_distr
|
||
|
.
|
||
Exercise 6.3
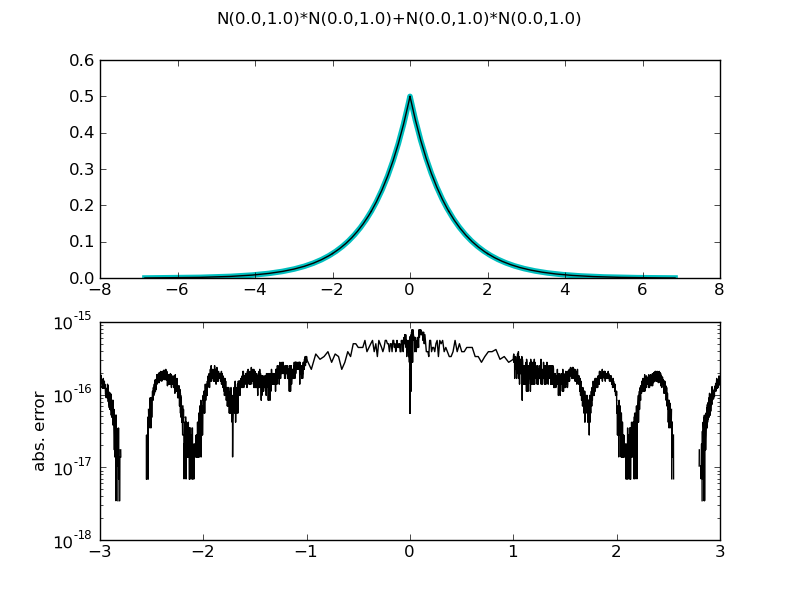
| ... d = NormalDistr() * NormalDistr() + NormalDistr() * NormalDistr()
figure()
demo_distr(d, theoretical = LaplaceDistr())
|
||
|
.
|
||
============= summary =============
N(0.0,1.0)*N(0.0,1.0)+N(0.0,1.0)*N(0.0,1.0)
mean = 0.0 +/- 0
std = 1.414213562373007 +/- 8.84e-14
var = 1.9999999999997509 +/- 2.5e-13
median = 0.0 +/- 0
medianad = 0.69314718056027658 +/- 2.72e-13
iqrange(0.025) = 5.9914645471079648 +/- 3.55e-15
int_err = -8.8817841970012523e-16 +/- 8.88e-16
max. abs. error 7.77156117238e-16
max. rel. error 1.62513294066e-13
| ... |
||
|
.
|
||
Example 7.3.1
| ... w1 = WeibullDistr(2)
w2 = WeibullDistr(3)
figure()
demo_distr(w1 * w2)
|
||
|
.
|
||
============= summary =============
Weibull(2,1)*Weibull(3,1)
mean = 0.79138248703
std = 0.525793735387
var = 0.276459052173
median = 0.682577502361
medianad = 0.319650838745
iqrange(0.025) = 1.98654059159
range = (0.0, inf)
ci(0.05) = (0.10350362375091107, 2.0900442153396623)
int_err = -6.66133814775e-16

| ... |
||
|
.
|
||
Example 7.3.2
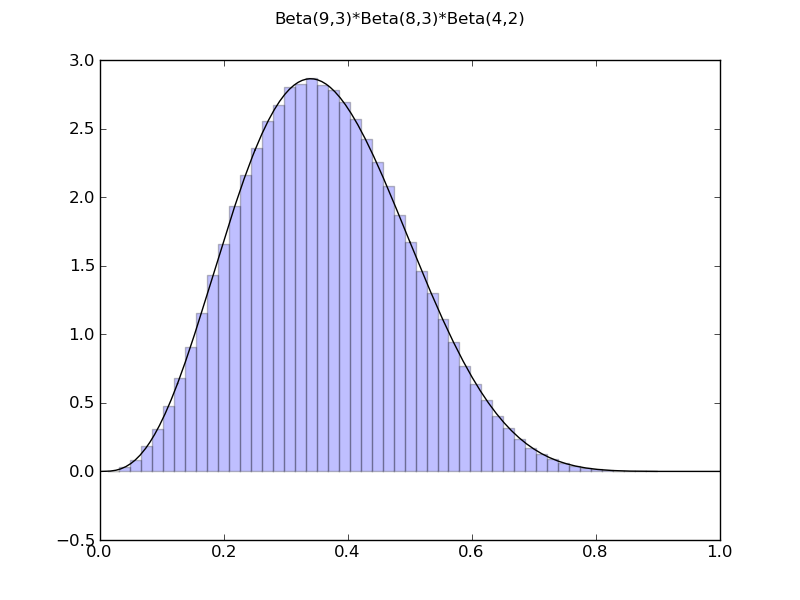
| ... x1 = BetaDistr(9,3)
x2 = BetaDistr(8,3)
x3 = BetaDistr(4,2)
figure()
demo_distr(x1 * x2 * x3)
|
||
|
.
|
||
============= summary =============
Beta(9,3)*Beta(8,3)*Beta(4,2)
mean = 0.363636363636
std = 0.132735620281
var = 0.0176187448915
median = 0.35667005299
medianad = 0.0934881404244
iqrange(0.025) = 0.509066944234
range = (0.0, 1.0)
ci(0.05) = (0.12839999335479427, 0.63746693758840289)
int_err = 4.4408920985e-16
| ... |
||
|
.
|
||
Example 8.6.1
| ... x1 = abs(NormalDistr(0, 1.5))
x2 = GammaDistr(.2,1)
x3 = ExponentialDistr(1.0/0.4)
x4 = abs(NormalDistr(0, 2))
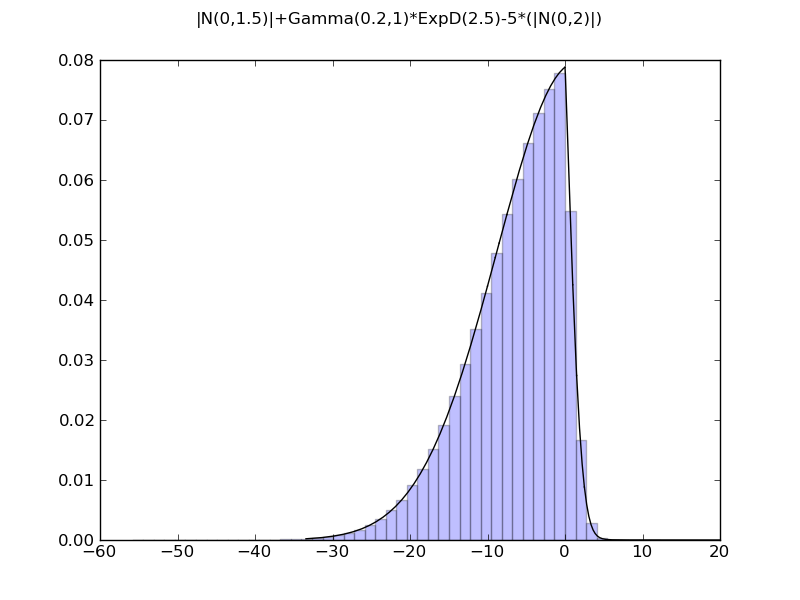
d = x1+x2*x3-5*x4
figure()
demo_distr(d, xmax=20)
|
||
|
.
|
||
============= summary =============
|N(0,1.5)|+Gamma(0.2,1)*ExpD(2.5)-5*(|N(0,2)|)
mean = -6.70192384093
std = 6.10127028473
var = 37.2254990874
median = -5.4985651725
medianad = 4.00784227757
iqrange(0.025) = 22.6566642056
range = (-inf, inf)
ci(0.05) = (-21.230601062235511, 1.4260631433811117)
int_err = 1.42336354729e-05
| ... exm = -6.7020187668243558
print "exact mean =", exm, "err =", d.mean() - exm
|
||
|
.
|
||
exact mean = -6.70201876682 err = 9.49258993517e-05
| ... |
||
|
.
|
||
Example 8.7.1
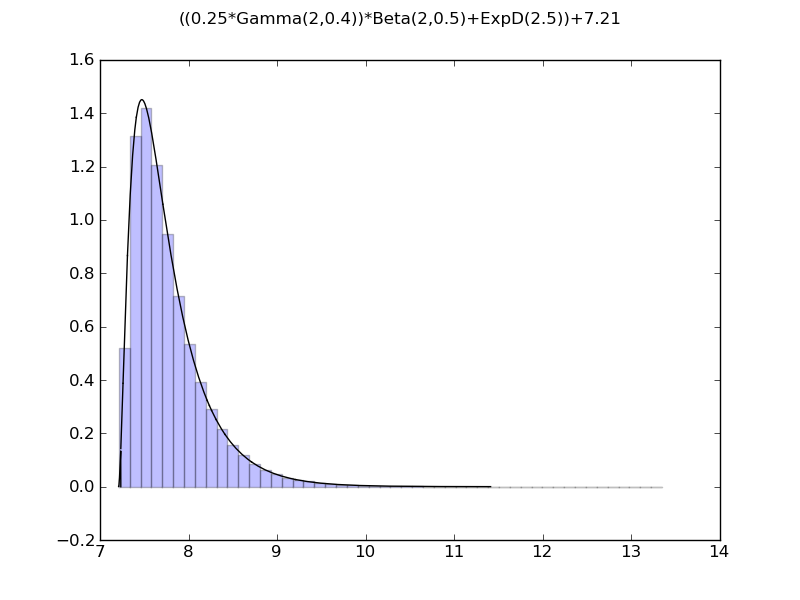
poles at nonzero locations, not handled well yet
| ... x1 = GammaDistr(2,0.4)
x2 = BetaDistr(2,0.5)
x3 = ExponentialDistr(1.0/0.4)
d = 0.25*x1*x2 + x3 + 7.21
figure()
demo_distr(d)
|
||
|
.
|
||
============= summary =============
((0.25*Gamma(2,0.4))*Beta(2,0.5)+ExpD(2.5))+7.21
mean = 7.75970503409
std = 0.418813441076
var = 0.175404698426
median = 7.66141788854
medianad = 0.218286122257
iqrange(0.025) = 1.59866007665
range = (7.21, inf)
ci(0.05) = (7.2912572969832476, 8.8899173736370951)
int_err = 0.00131493478447
| ... |
||
|
.
|
||
Example 8.13.1
| ... d = BetaDistr(5,2) * BetaDistr(6,2) * BetaDistr(6,3)
figure()
demo_distr(d)
|
||
|
.
|
||
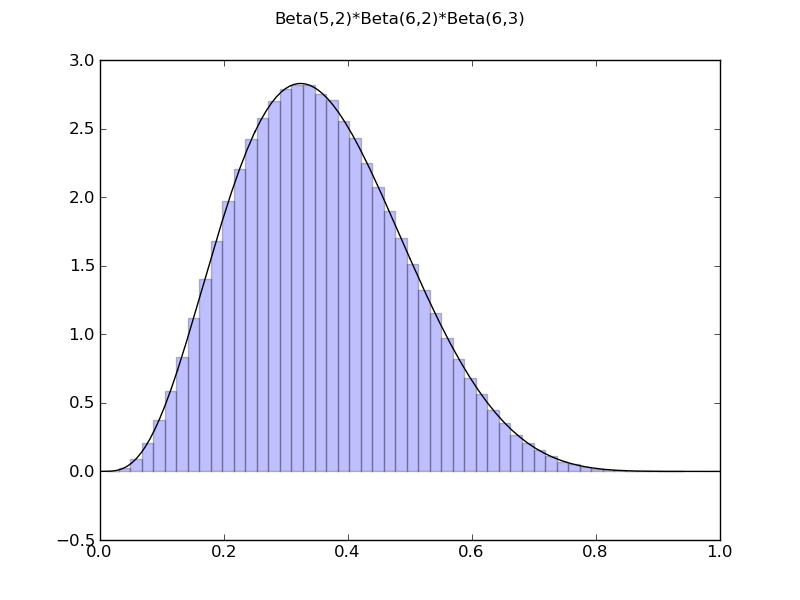
============= summary =============
Beta(5,2)*Beta(6,2)*Beta(6,3)
mean = 0.357142857143
std = 0.135212103471
var = 0.0182823129252
median = 0.34765738999
medianad = 0.0949836826404
iqrange(0.025) = 0.517387403603
range = (0.0, 1.0)
ci(0.05) = (0.12427444435865699, 0.64166184796133963)
int_err = -8.881784197e-16
| ... |
||
|
.
|
||
Example 8.13.2
| ... d = abs(NormalDistr()) + ExponentialDistr()
figure()
demo_distr(d)
|
||
|
.
|
||
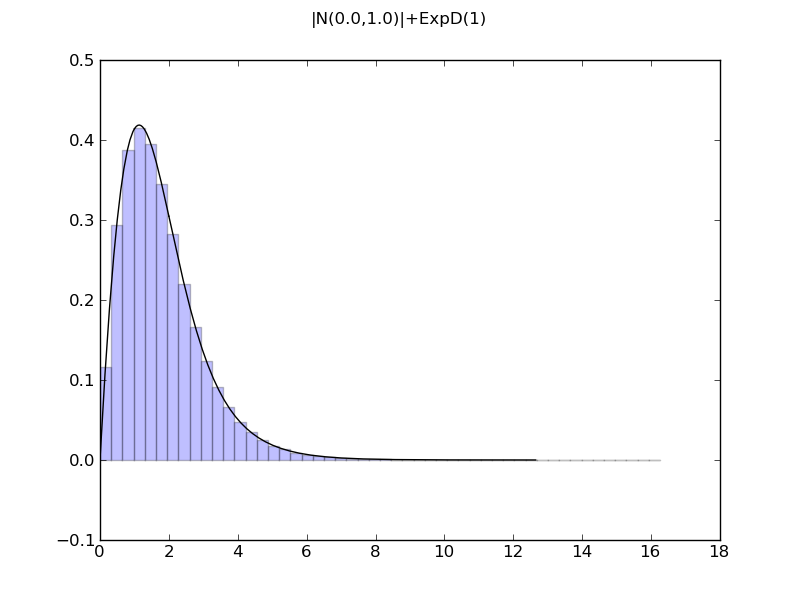
============= summary =============
|N(0.0,1.0)|+ExpD(1)
mean = 1.7978845608
std = 1.16763874021
var = 1.36338022763
median = 1.56615756659
medianad = 0.684852737875
iqrange(0.025) = 4.44721795288
range = (0.0, inf)
ci(0.05) = (0.26203081525543453, 4.7092487681369528)
int_err = -8.881784197e-16
| ... show()
|
||
|
.
|
||
