CHAPTER 3 - SUMS
| ... from functools import partial
import numpy
from pylab import figure, show
from pacal import *
|
||
|
.
|
||
Using compiled interpolation routine
| ... from pacal.distr import demo_distr
|
||
|
.
|
||
Figure 3.1.1
| ... figure()
demo_distr(UniformDistr(0,1) + UniformDistr(0,1),
theoretical = lambda x: x * ((x >= 0) & (x < 1)) + (2-x) * ((x >= 1) & (x <= 2)))
|
||
|
.
|
||
============= summary =============
U(0,1)+U(0,1)
mean = 1.0
std = 0.408248290464
var = 0.166666666667
median = 1.0
medianad = 0.292893218813
iqrange(0.025) = 1.5527864045
range = (0.0, 2.0)
ci(0.05) = (0.22360679774999898, 1.7763932022500011)
int_err = 0.0
max. abs. error 2.22044604925e-16
max. rel. error 8.71670994575e-16
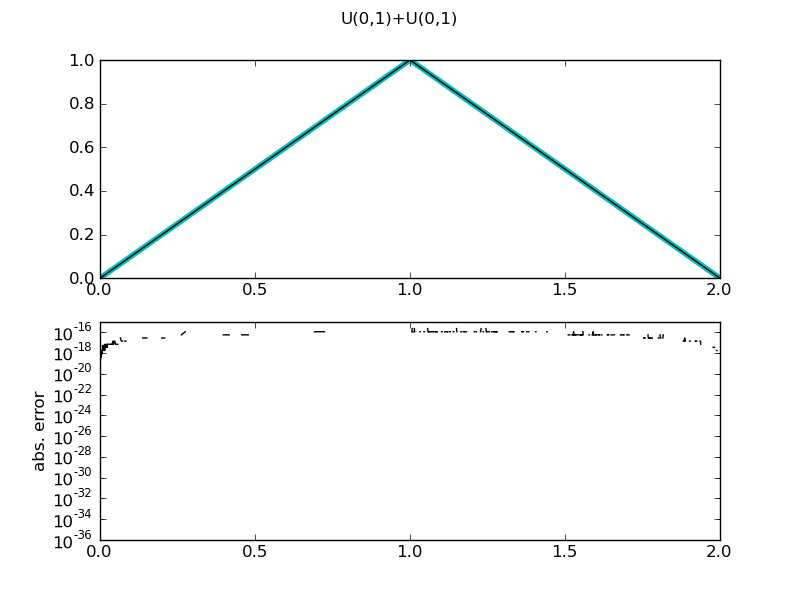
Figure 3.1.2
| ... figure()
demo_distr(UniformDistr(0,1) - UniformDistr(0,1),
theoretical = lambda x: (x+1) * ((x >= -1) & (x < 0)) + (1-x) * ((x >= 0) & (x <= 1)))
|
||
|
.
|
||
============= summary =============
U(0,1)-U(0,1)
mean = -2.77555756156e-17
std = 0.408248290464
var = 0.166666666667
median = 0.0
medianad = 0.292893218813
iqrange(0.025) = 1.5527864045
range = (-1.0, 1.0)
ci(0.05) = (-0.77639320225000097, 0.77639320225000086)
int_err = 0.0
max. abs. error 3.33066907388e-16
max. rel. error 3.93803481559e-16

| ... |
||
|
.
|
||
Section 3.2.2
| ... figure()
demo_distr(ChiSquareDistr(1) + ChiSquareDistr(1),
theoretical = ExponentialDistr(0.5))
|
||
|
.
|
||
============= summary =============
Chi2(1)+Chi2(1)
mean = 2.0000000000000018 +/- 4.44e-16
std = 2.0000000000000009 +/- 8.88e-16
var = 4.0000000000000036 +/- 2.66e-15
median = 1.3862943611199283 +/- 3.77e-14
medianad = 0.96242365011952014 +/- 3.13e-13
iqrange(0.025) = 7.3271232922592242 +/- 1.09e-13
int_err = -4.4408920985006262e-16 +/- 4.44e-16
max. abs. error 8.881784197e-16
max. rel. error 3.19028152637e-14

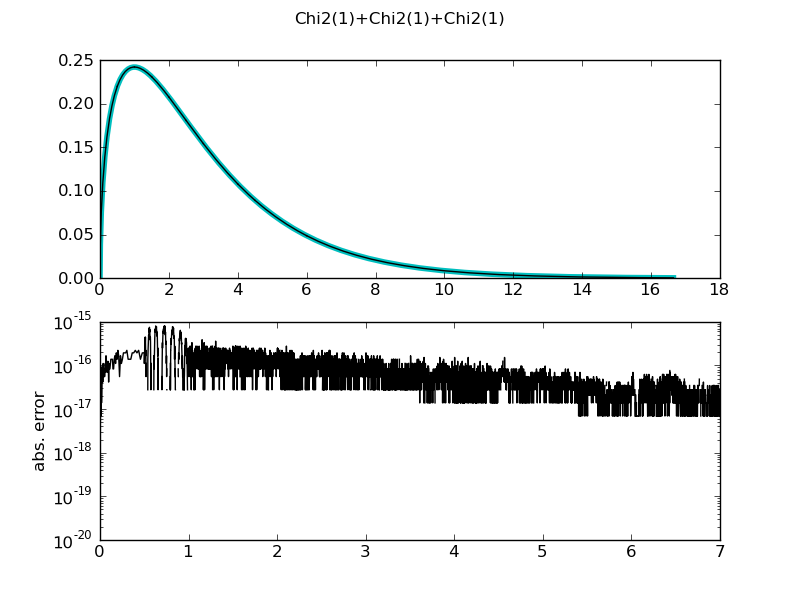
| ... figure()
demo_distr(ChiSquareDistr(1) + ChiSquareDistr(1) + ChiSquareDistr(1),
theoretical = ChiSquareDistr(3))
|
||
|
.
|
||
============= summary =============
Chi2(1)+Chi2(1)+Chi2(1)
mean = 2.9999999999997833 +/- 2.18e-13
std = 2.4494897427818314 +/- 1.35e-12
var = 5.9999999999934017 +/- 6.6e-12
median = 2.3659738843753635 +/- 2.66e-14
medianad = 1.3401286628171192 +/- 8.66e-15
iqrange(0.025) = 9.1326083218731249 +/- 8.9e-13
int_err = 5.3290705182007514e-15 +/- 5.33e-15
max. abs. error 8.60422844084e-16
max. rel. error 2.70282273594e-07
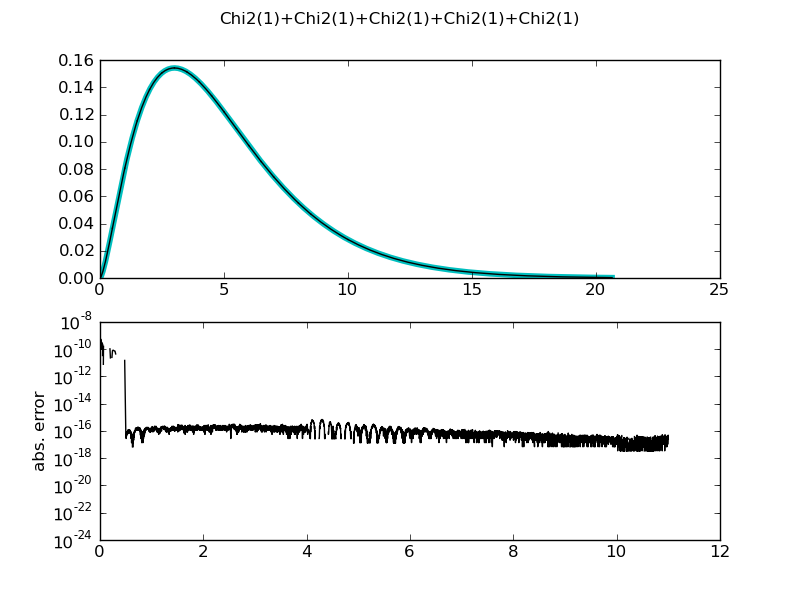
| ... figure()
demo_distr(ChiSquareDistr(1) + ChiSquareDistr(1) + ChiSquareDistr(1) + ChiSquareDistr(1),
theoretical = ChiSquareDistr(4))
|
||
|
.
|
||
============= summary =============
Chi2(1)+Chi2(1)+Chi2(1)+Chi2(1)
mean = 4.0000000000000222 +/- 2.13e-14
std = 2.8284271247462551 +/- 6.39e-14
var = 8.0000000000003677 +/- 3.61e-13
median = 3.3566939800333202 +/- 0
medianad = 1.6398381276523741 +/- 1.44e-14
iqrange(0.025) = 10.658868224789833 +/- 2.01e-13
int_err = -1.7763568394002505e-15 +/- 1.78e-15
max. abs. error 7.07767178199e-16
max. rel. error 16652.3453694

| ... figure()
demo_distr(ChiSquareDistr(1) + ChiSquareDistr(1) + ChiSquareDistr(1) + ChiSquareDistr(1) + ChiSquareDistr(1),
theoretical = ChiSquareDistr(5))
|
||
|
.
|
||
============= summary =============
Chi2(1)+Chi2(1)+Chi2(1)+Chi2(1)+Chi2(1)
mean = 5.0000000000000533 +/- 5.15e-14
std = 3.1622776601684954 +/- 1.15e-13
var = 10.000000000000734 +/- 7.25e-13
median = 4.3514601910956703 +/- 1.45e-13
medianad = 1.894722775885864 +/- 1.09e-14
iqrange(0.025) = 12.001290380545083 +/- 1.6e-12
int_err = 1.7541523789077473e-14 +/- 1.75e-14
max. abs. error 3.00356863824e-09
max. rel. error 43388889.1227
| ... figure()
demo_distr(ChiSquareDistr(1) + ChiSquareDistr(3),
theoretical = ChiSquareDistr(4))
|
||
|
.
|
||
============= summary =============
Chi2(1)+Chi2(3)
mean = 4.0000000000000018 +/- 8.88e-16
std = 2.8284271247461912 +/- 0
var = 8.0000000000000071 +/- 0
median = 3.3566939800331634 +/- 1.57e-13
medianad = 1.6398381276523215 +/- 3.82e-14
iqrange(0.025) = 10.658868224789826 +/- 2.08e-13
int_err = -4.4408920985006262e-16 +/- 4.44e-16
max. abs. error 4.16333634234e-16
max. rel. error 16652.3453694

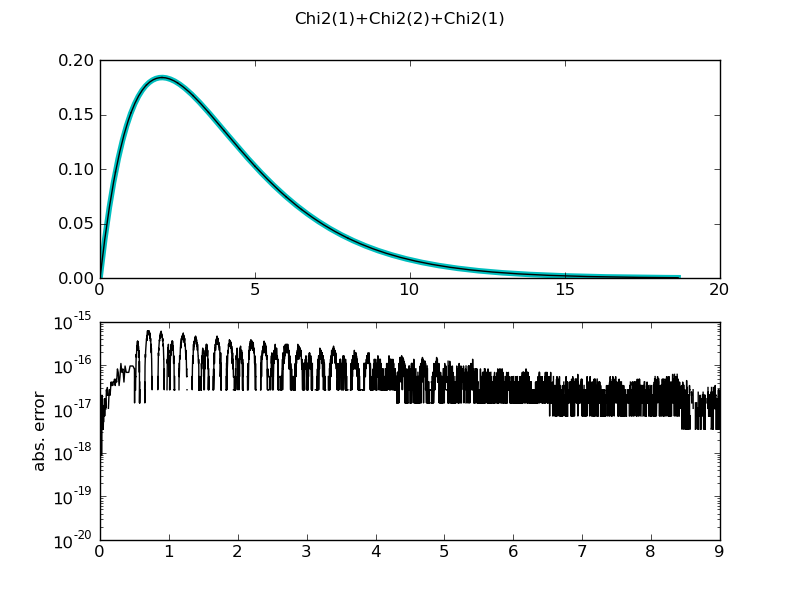
| ... figure()
demo_distr(ChiSquareDistr(1) + (ChiSquareDistr(2)+ChiSquareDistr(1)),
theoretical = ChiSquareDistr(4))
|
||
|
.
|
||
============= summary =============
Chi2(1)+Chi2(2)+Chi2(1)
mean = 3.9999999999999716 +/- 2.93e-14
std = 2.8284271247460095 +/- 1.82e-13
var = 7.9999999999989786 +/- 1.03e-12
median = 3.356693980033322 +/- 1.78e-15
medianad = 1.6398381276523752 +/- 1.55e-14
iqrange(0.025) = 10.658868224789858 +/- 1.76e-13
int_err = 1.1102230246251565e-16 +/- 1.11e-16
max. abs. error 6.66133814775e-16
max. rel. error 27754.5756156
| ... figure()
demo_distr(ChiSquareDistr(2) + ChiSquareDistr(2),
theoretical = ChiSquareDistr(4))
|
||
|
.
|
||
============= summary =============
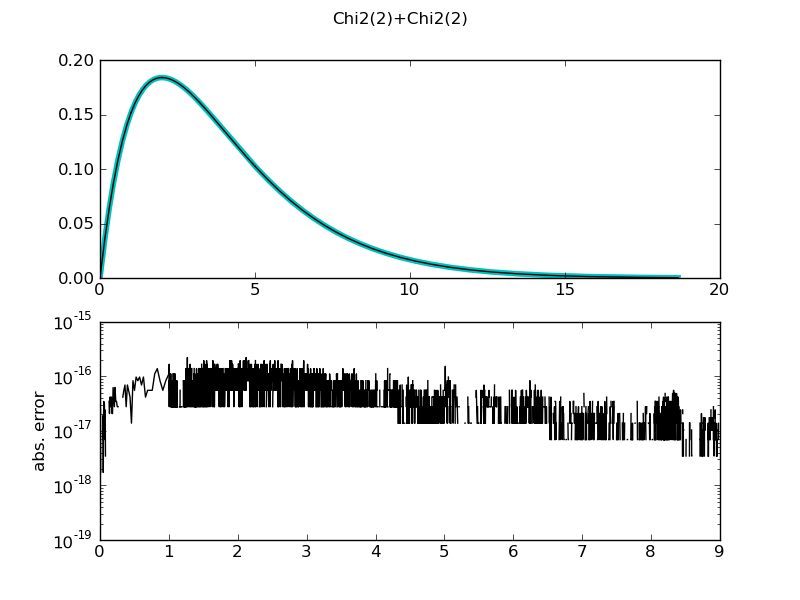
Chi2(2)+Chi2(2)
mean = 4.0000000000000018 +/- 8.88e-16
std = 2.8284271247461912 +/- 0
var = 8.0000000000000071 +/- 0
median = 3.3566939800333193 +/- 8.88e-16
medianad = 1.6398381276523744 +/- 1.47e-14
iqrange(0.025) = 10.658868224789792 +/- 2.42e-13
int_err = -4.4408920985006262e-16 +/- 4.44e-16
max. abs. error 3.16437956567e-16
max. rel. error 55510.1512313
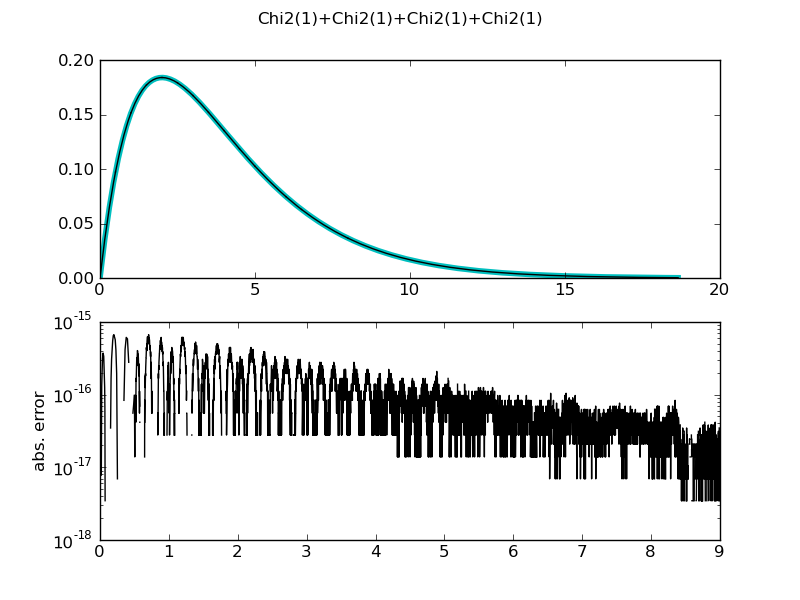
| ... figure()
demo_distr((ChiSquareDistr(1)+ChiSquareDistr(1)) + (ChiSquareDistr(1)+ChiSquareDistr(1)),
theoretical = ChiSquareDistr(4))
|
||
|
.
|
||
============= summary =============
Chi2(1)+Chi2(1)+Chi2(1)+Chi2(1)
mean = 3.9999999999999925 +/- 8.44e-15
std = 2.8284271247461228 +/- 6.84e-14
var = 7.9999999999996199 +/- 3.87e-13
median = 3.3566939800333202 +/- 0
medianad = 1.6398381276523741 +/- 1.44e-14
iqrange(0.025) = 10.658868224789801 +/- 2.33e-13
int_err = -6.6613381477509392e-16 +/- 6.66e-16
max. abs. error 6.66133814775e-16
max. rel. error 1.72329583954e-13
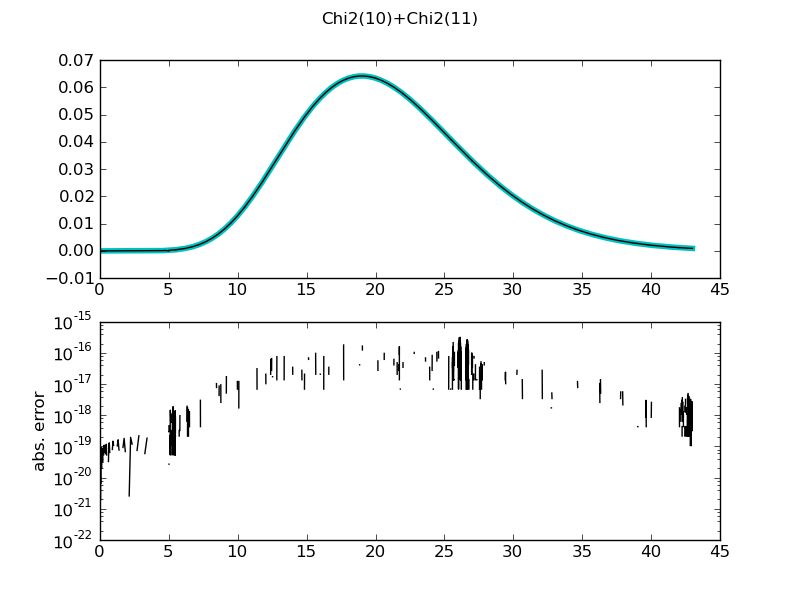
| ... figure()
demo_distr(ChiSquareDistr(10) + ChiSquareDistr(11),
theoretical = ChiSquareDistr(21))
|
||
|
.
|
||
============= summary =============
Chi2(10)+Chi2(11)
mean = 20.999999999999986 +/- 7.11e-14
std = 6.4807406984078577 +/- 1.15e-14
var = 41.999999999999972 +/- 1.49e-13
median = 20.33722756354793 +/- 2.49e-14
medianad = 4.2573833922862141 +/- 1.95e-14
iqrange(0.025) = 25.195978123204466 +/- 4.44e-13
int_err = 7.7715611723760958e-16 +/- 7.77e-16
max. abs. error 5.34294830601e-16
max. rel. error 1.22696011031e+179
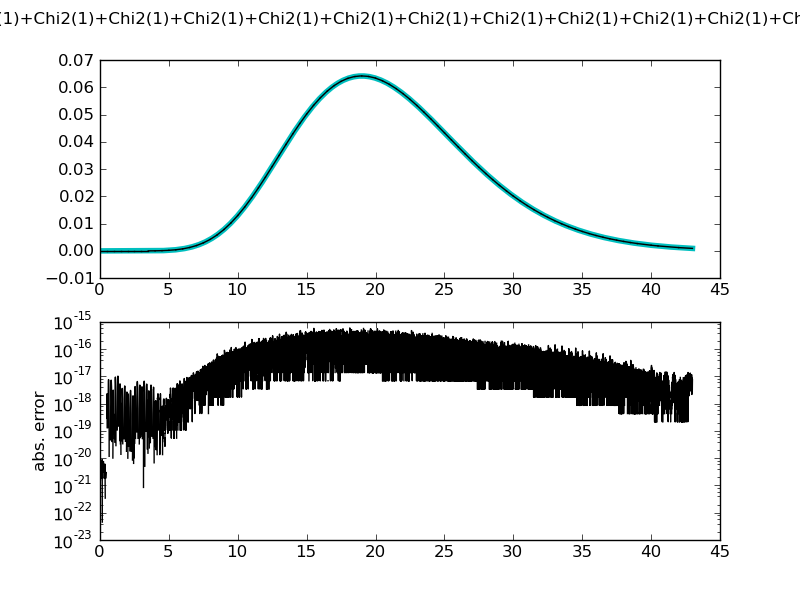
| ... cd = ChiSquareDistr(4)
for i in xrange(17):
cd = cd + ChiSquareDistr(1)
figure()
demo_distr(cd, theoretical = ChiSquareDistr(21))
|
||
|
.
|
||
============= summary =============
Chi2(4)+Chi2(1)+Chi2(1)+Chi2(1)+Chi2(1)+Chi2(1)+Chi2(1)+Chi2(1)+Chi2(1)+Chi2(1)+Chi2(1)+Chi2(1)+Chi2(1)+Chi2(1)+Chi2(1)+Chi2(1)+Chi2(1)+Chi2(1)
mean = 21.000000000000114 +/- 5.68e-14
std = 6.4807406984079794 +/- 1.1e-13
var = 42.000000000001542 +/- 1.42e-12
median = 20.337227563547888 +/- 1.78e-14
medianad = 4.2573833922866253 +/- 4.31e-13
iqrange(0.025) = 25.195978123203766 +/- 2.56e-13
int_err = -4.6629367034256575e-15 +/- 4.66e-15
max. abs. error 6.24500451352e-16
max. rel. error 9.58460811966e+178
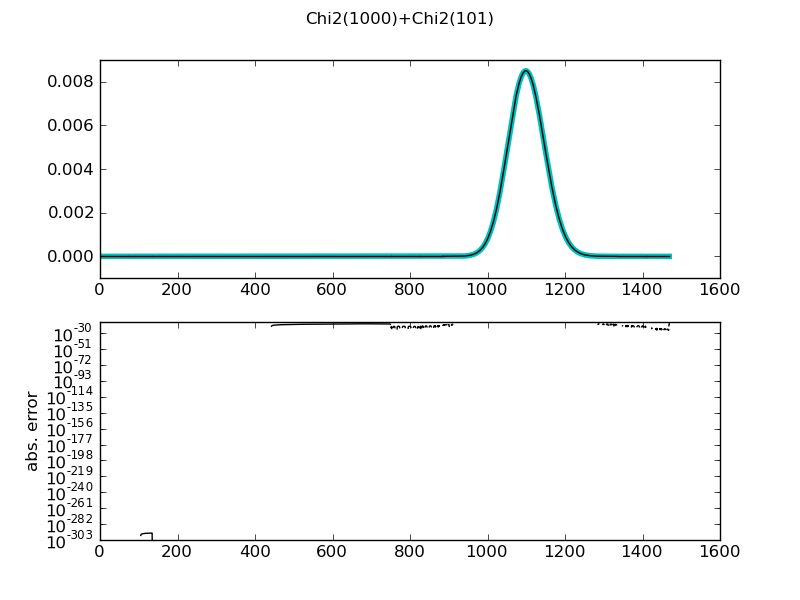
| ... figure()
demo_distr(ChiSquareDistr(1000) + ChiSquareDistr(101),
theoretical = ChiSquareDistr(1101))
|
||
|
.
|
||
============= summary =============
Chi2(1000)+Chi2(101)
mean = 1101.0000000001796 +/- 5.39e-10
std = 46.925472826604349 +/- 1.05e-11
var = 2202.0000000003829 +/- 9.88e-10
median = 1100.3334051450893 +/- 2.32e-11
medianad = 31.635143878247124 +/- 1.58e-11
iqrange(0.025) = 183.91516747912681 +/- 3.15e-10
int_err = -1.6320278461989801e-13 +/- 1.63e-13
max. abs. error 8.05085165201e-15
max. rel. error 1.7541615054e+272
| ... |
||
|
.
|
||
Section 3.3.1
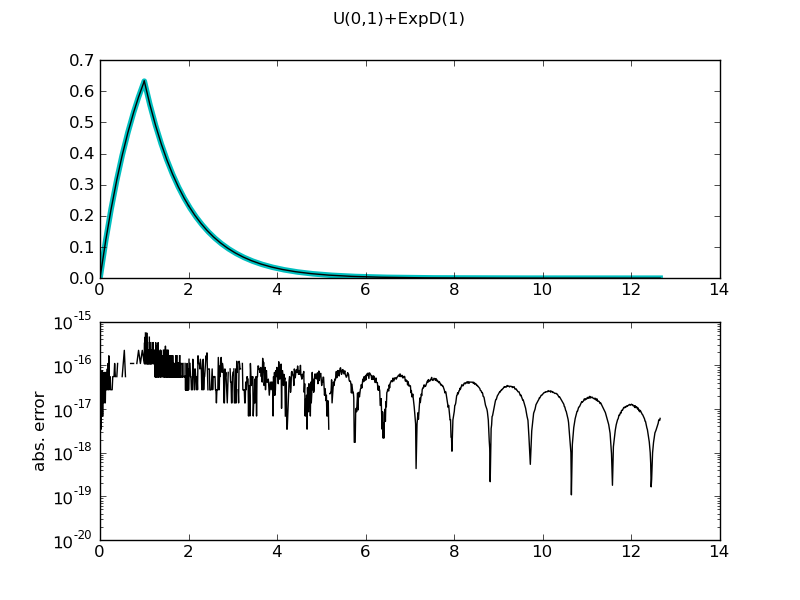
| ... figure()
demo_distr(UniformDistr(0,1) + ExponentialDistr(),
theoretical = lambda x: -numpy.exp(-x) + (x >= 0)*(x <= 1) + (x > 1)*numpy.exp(-x+1))
|
||
|
.
|
||
============= summary =============
U(0,1)+ExpD(1)
mean = 1.5
std = 1.04083299973
var = 1.08333333333
median = 1.23447203517
medianad = 0.521465208667
iqrange(0.025) = 3.99794423208
range = (0.0, inf)
ci(0.05) = (0.23226007664824921, 4.2302043087268375)
int_err = -4.4408920985e-16
max. abs. error 5.55111512313e-16
max. rel. error 0.477178385421
Exercise 3.10
| ... figure()
demo_distr(ExponentialDistr() - ExponentialDistr(),
theoretical = lambda x: numpy.exp(-numpy.abs(x)) / 2)
|
||
|
.
|
||
============= summary =============
ExpD(1)-ExpD(1)
mean = 2.77555756156e-16
std = 1.41421356237
var = 2.0
median = 0.0
medianad = 0.69314718056
iqrange(0.025) = 5.99146454711
range = (-inf, inf)
ci(0.05) = (-2.9957322735543057, 2.9957322735539758)
int_err = -4.4408920985e-16
max. abs. error 4.4408920985e-16
max. rel. error 2.94101467942e-13

| ... |
||
|
.
|
||
Exercise 3.11
| ... figure()
demo_distr(CauchyDistr() + CauchyDistr(), theoretical = CauchyDistr(gamma = 2))
|
||
|
.
|
||
============= summary =============
Cauchy(0.0,1.0)+Cauchy(0.0,1.0)
mean = nan +/- 0
std = nan +/- 0
var = nan +/- 0
median = 0.0 +/- 1.33e-15
medianad = 2.0 +/- 1.33e-15
iqrange(0.025) = 50.824818944698336 +/- 8.53e-14
int_err = -4.4408920985006262e-16 +/- 4.44e-16
max. abs. error 1.94289029309e-16
max. rel. error 2.60658794771e-15

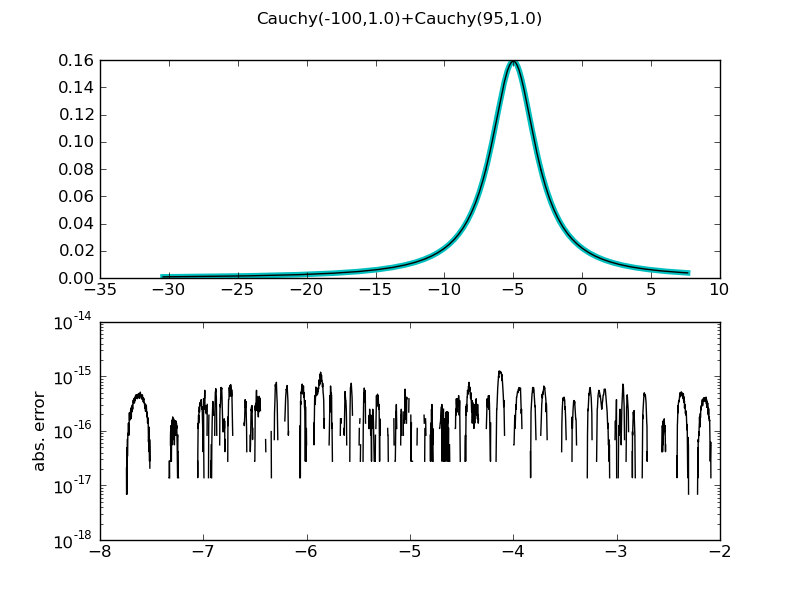
| ... figure()
demo_distr(CauchyDistr(center = -100) + CauchyDistr(center = 95), theoretical = CauchyDistr(gamma = 2, center = -5))
|
||
|
.
|
||
============= summary =============
Cauchy(-100,1.0)+Cauchy(95,1.0)
mean = nan +/- 0
std = nan +/- 0
var = nan +/- 0
median = -5.0 +/- 1.78e-15
medianad = 2.0 +/- 1.78e-15
iqrange(0.025) = 50.824818944698507 +/- 1.21e-13
int_err = 3.1086244689504383e-14 +/- 3.11e-14
max. abs. error 1.31838984174e-15
max. rel. error 1.2601539897e-14
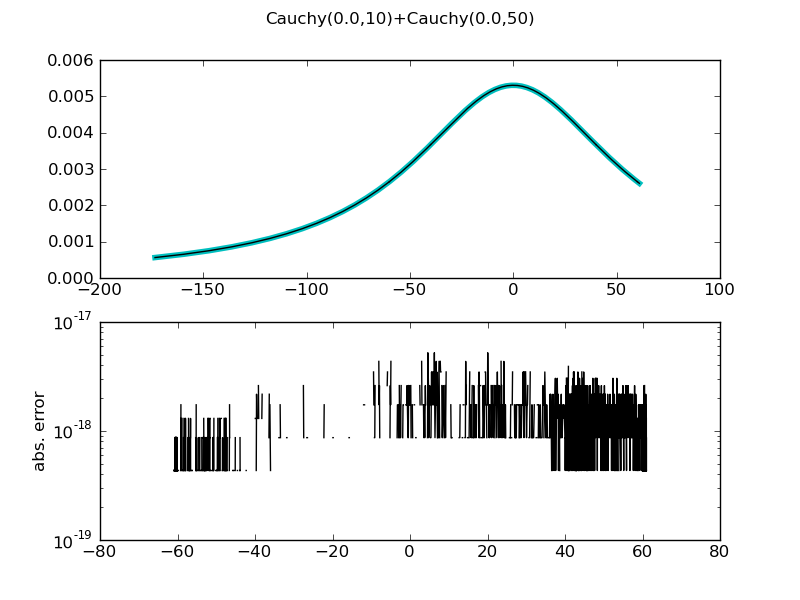
| ... figure()
demo_distr(CauchyDistr(gamma = 10) + CauchyDistr(gamma = 50), theoretical = CauchyDistr(gamma = 60))
|
||
|
.
|
||
============= summary =============
Cauchy(0.0,10)+Cauchy(0.0,50)
mean = nan +/- 0
std = nan +/- 0
var = nan +/- 0
median = -3.5527136788005009e-14 +/- 7.11e-15
medianad = 59.999999999999964 +/- 7.11e-15
iqrange(0.025) = 1524.7445683409528 +/- 4.55e-13
int_err = -4.4408920985006262e-16 +/- 4.44e-16
max. abs. error 5.20417042793e-18
max. rel. error 1.4560046931e-15
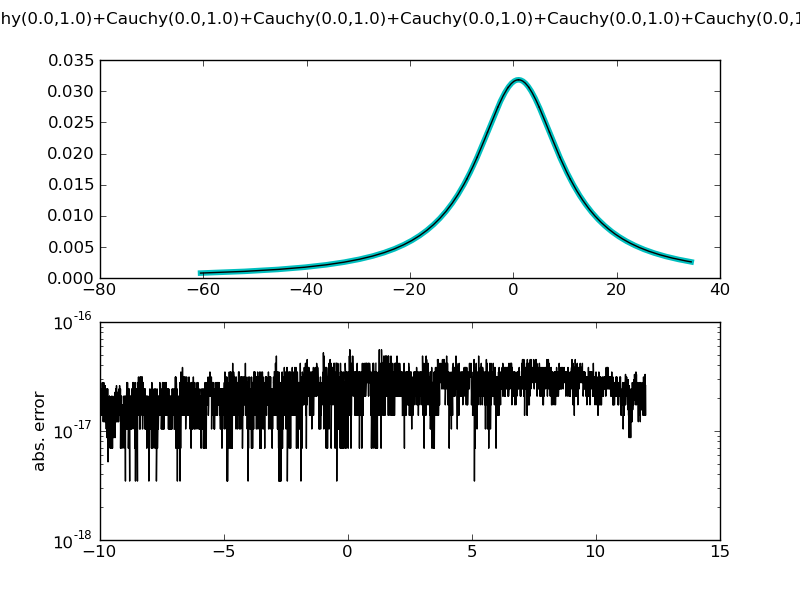
| ... figure()
c = CauchyDistr(center = 1)
for i in xrange(9):
c += CauchyDistr()
demo_distr(c, theoretical = CauchyDistr(gamma = 10, center = 1))
|
||
|
.
|
||
============= summary =============
Cauchy(1,1.0)+Cauchy(0.0,1.0)+Cauchy(0.0,1.0)+Cauchy(0.0,1.0)+Cauchy(0.0,1.0)+Cauchy(0.0,1.0)+Cauchy(0.0,1.0)+Cauchy(0.0,1.0)+Cauchy(0.0,1.0)+Cauchy(0.0,1.0)
mean = nan +/- 0
std = nan +/- 0
var = nan +/- 0
median = 1.0 +/- 7.11e-15
medianad = 10.0 +/- 7.11e-15
iqrange(0.025) = 254.12409472348259 +/- 9.44e-12
int_err = -2.2204460492503131e-15 +/- 2.22e-15
max. abs. error 5.55111512313e-17
max. rel. error 5.98067554181e-15
| ... |
||
|
.
|
||
Exercise 3.12 Exact formula for sum of 'N' uniform random variables
'warning': this formula is very inaccurate for large n! much worse than our results!
| ... from numpy import ceil, isscalar, zeros_like, asfarray
def uniform_sum_pdf(n, xx):
if isscalar(xx):
xx = asfarray(xx)
y = zeros_like(asfarray(xx))
for j, x in enumerate(xx):
r = int(ceil(x))
if r <= 0 or r > n:
y[j] = 0
else:
nck = 1
pdf = 0.0
for k in xrange(r):
pdf += (-1)**k * nck * (x-k)**(n-1)
nck *= n - k
nck /= k + 1
for i in xrange(2, n):
pdf /= i
y[j] = pdf
return y
|
||
|
.
|
||
| ... u = UniformDistr(0,1) + UniformDistr(0,1)
figure()
demo_distr(u, theoretical = partial(uniform_sum_pdf, 2))
|
||
|
.
|
||
============= summary =============
U(0,1)+U(0,1)
mean = 1.0
std = 0.408248290464
var = 0.166666666667
median = 1.0
medianad = 0.292893218813
iqrange(0.025) = 1.5527864045
range = (0.0, 2.0)
ci(0.05) = (0.22360679774999898, 1.7763932022500011)
int_err = 0.0
max. abs. error 2.22044604925e-16
max. rel. error 8.71670994575e-16

| ... for i in xrange(2):
u += UniformDistr(0,1)
figure()
demo_distr(u, theoretical = partial(uniform_sum_pdf, 3+i))
|
||
|
.
|
||
============= summary =============
U(0,1)+U(0,1)+U(0,1)+U(0,1)
mean = 2.0
std = 0.57735026919
var = 0.333333333333
median = 2.0
medianad = 0.402726641789
iqrange(0.025) = 2.23977652641
range = (0.0, 4.0)
ci(0.05) = (0.88011173679339316, 3.1198882632066072)
int_err = 1.11022302463e-16
max. abs. error 2.46738325843e-15
max. rel. error 4.94281050867e+16

| ... u = UniformDistr(0,1)
for i in xrange(49):
u += UniformDistr(0,1)
figure()
demo_distr(u, theoretical = partial(uniform_sum_pdf, i+2))
|
||
|
.
|
||
============= summary =============
U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)+U(0,1)
mean = 25.0
std = 2.04124145232
var = 4.16666666667
median = 25.0
medianad = 1.38031779155
iqrange(0.025) = 7.99475034965
range = (0.0, 50.0)
ci(0.05) = (21.002624825173744, 28.9973751748262)
int_err = -1.33226762955e-15
max. abs. error 25521117600.1
max. rel. error 3.72514471857e+284

| ... |
||
|
.
|
||
Exercise 3.15
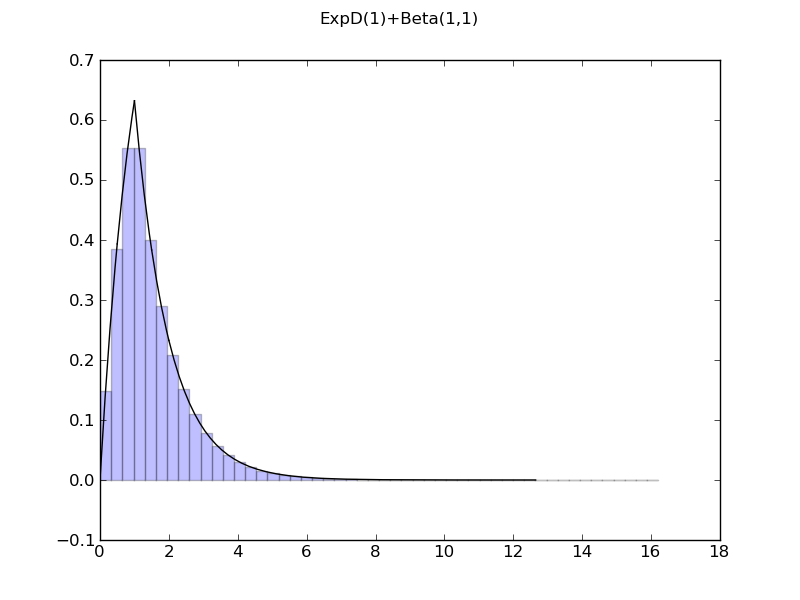
| ... figure()
demo_distr(ExponentialDistr() + BetaDistr(1,1))
|
||
|
.
|
||
============= summary =============
ExpD(1)+Beta(1,1)
mean = 1.5
std = 1.04083299973
var = 1.08333333333
median = 1.23447203517
medianad = 0.521465208667
iqrange(0.025) = 3.99794423208
range = (0.0, inf)
ci(0.05) = (0.23226007664824938, 4.2302043087268375)
int_err = -4.4408920985e-16
Exercise 3.16
| ... figure()
demo_distr(UniformDistr(0,1) + ExponentialDistr() + ChiSquareDistr(4),
theoretical = lambda x: (x>=0) * ((x<=1) + (x>1)*(exp(-x+1) + (x-1)*exp(-(x-1)/2)) - exp(-x) - x*exp(-x/2)))
|
||
|
.
|
||
============= summary =============
U(0,1)+ExpD(1)+Chi2(4)
mean = 5.5
std = 3.01385688667
var = 9.08333333333
median = 4.90537342209
medianad = 1.80315703259
iqrange(0.025) = 11.5006024874
range = (0.0, inf)
ci(0.05) = (1.4322827733366463, 12.932885260784827)
int_err = -4.4408920985e-16
max. abs. error 3.95516952523e-16
max. rel. error 1.41725093647

Exercise 3.18
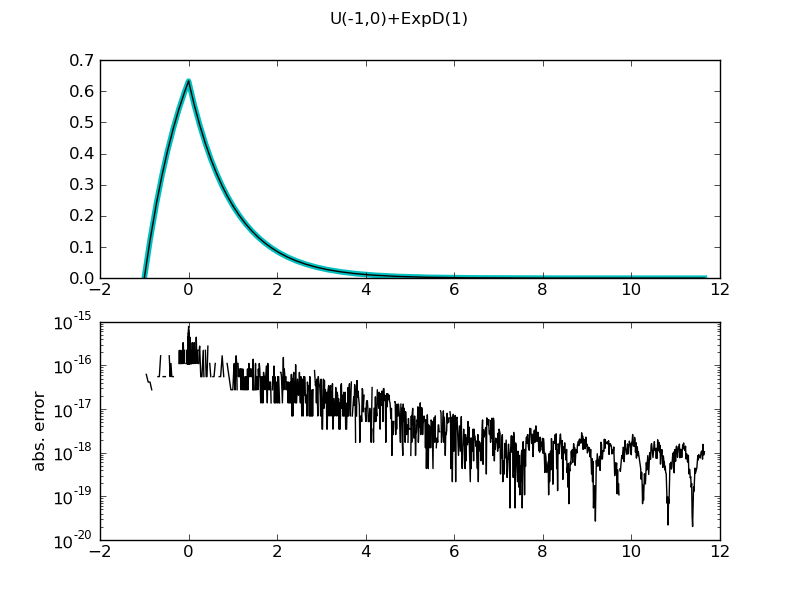
| ... figure()
demo_distr(UniformDistr(-1,0) + ExponentialDistr(),
theoretical = lambda x: -numpy.exp(-(x+1)) + (x >= -1)*(x <= 0) + (x > 0)*numpy.exp(-x))
|
||
|
.
|
||
============= summary =============
U(-1,0)+ExpD(1)
mean = 0.5
std = 1.04083299973
var = 1.08333333333
median = 0.234472035173
medianad = 0.521465208667
iqrange(0.025) = 3.99794423208
range = (-1.0, inf)
ci(0.05) = (-0.76773992335175079, 3.2302043087268375)
int_err = -4.4408920985e-16
max. abs. error 7.77156117238e-16
max. rel. error 2.72739600675e-13
Exercise 3.19
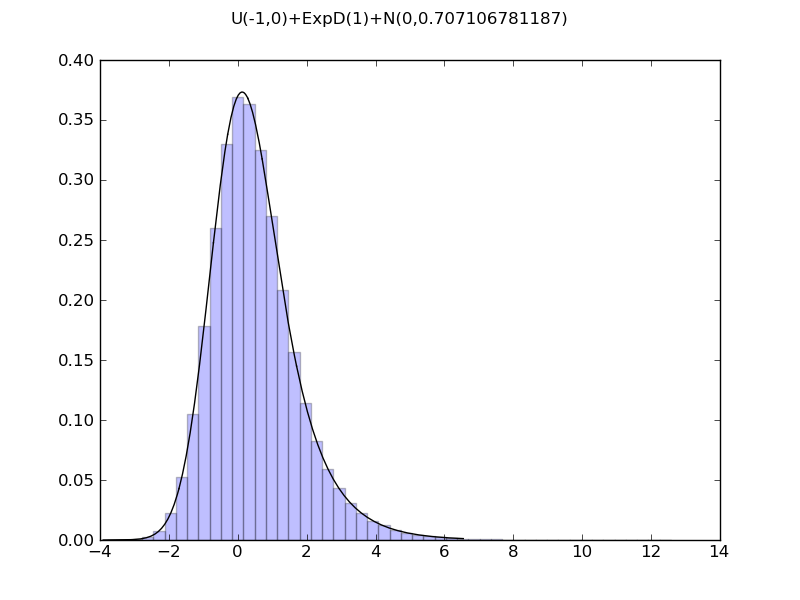
| ... figure()
demo_distr(UniformDistr(-1,0) + ExponentialDistr() + NormalDistr(0, 1.0/numpy.sqrt(2)))
|
||
|
.
|
||
============= summary =============
U(-1,0)+ExpD(1)+N(0,0.707106781187)
mean = 0.5
std = 1.25830573921
var = 1.58333333333
median = 0.342402641666
medianad = 0.743652229236
iqrange(0.025) = 4.99106223715
range = (-inf, inf)
ci(0.05) = (-1.5108582682799729, 3.480203968865454)
int_err = -2.22044604925e-16
| ... show()
|
||
|
.
|
||
