PaCAL - ProbAbilistic CALculator

What is PaCAL? PaCAL is a Python package which allows you to perform arithmetic on random variables just like you do with ordinary program variables. The variables can follow practically any distribution. Below are some examples which explain what the project is all about. See also our gallery.

Who's behind it? PaCAL is maintained by Szymon Jaroszewicz and Marcin Korzeń

How do I get started? Requirements and downloading information can be found in getting started.

Where can i find documentation? See examples included with the package and/or this paper:

Marcin Korzeń and Szymon Jaroszewicz. "PaCAL: A Python Package for Arithmetic Computations with Random Variables", Journal of Statistical Software, Volume 57, Issue 10, 2014.
The paper is available here.

How does it work? Discussion of the implementation and some theoretical guarantees are in this paper:

Szymon Jaroszewicz and Marcin Korzeń. "Arithmetic Operations on Independent Random Variables: A Numerical Approach", SIAM Journal on Scientific Computing, Volume 34, Issue 3, 2012, pages A1241-A1265.
The paper is available directly from SIAM or as a preprint.

Acknowledgements. PaCAL was supported by Research Grant no. 0685/B/T02/2009/37 of the Polish Ministry of Science and Higher Education (Ministerstwo Nauki i Szkolnictwa Wyższego). An inspiration for PaCAL was the Chebfun project.

Example 1

The code

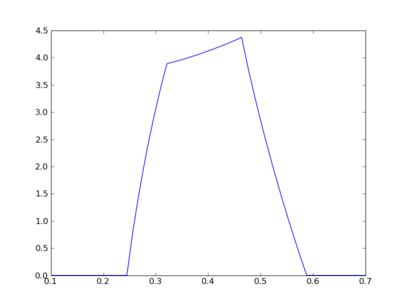
from pacal import *
dL = UniformDistr(1,3)
L0 = UniformDistr(9,11)
dT = NormalDistr(1,1)
K = dL / (L0 * dT)

K.plot()
show()

will produce the following chart:

This example corresponds to measuring the coefficient of thermal expansion K by measuring the initial length L0, the difference in length dL caused by temperature change dT. All quantities are measured with error, length with uniform error, temperature with normal error. The exact distribution of K has quite surprising shape.

Example 2

The code

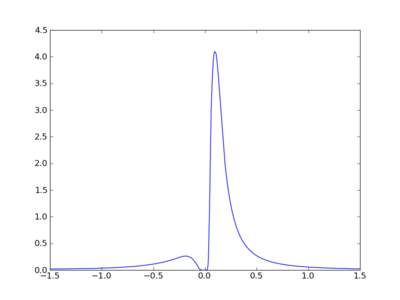
Y = UniformDistr(1,2)
X = UniformDistr(3,4)
A = atan(Y / X)

A.plot()
show()

will show

This example corresponds to measuring the angle A by measuring the opposite and adjacent sides of a triangle. Again the resulting distribution is quite 'strange'.